题目内容
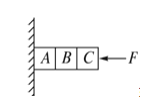
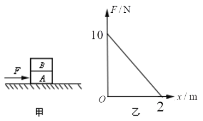
【题目】如图所示,水平传送带沿顺时针方向传动,质量为 m=1kg 的小物块由静止轻轻放上传送带,从 A 点随传送带运动到水平部分的最右端 B 点,经半圆轨道 C 点沿圆弧切线进入竖直光滑的半圆轨道,恰能做圆周运动.C 点在 B 点的正上方,D 点为轨道的最低点.小物块离开 D 点后,做平抛运动,恰好垂直于倾斜挡板打在挡板跟水平面相交的点.已知 D 点距水平面的高度 h=0.75m,倾斜挡板与水平面间的夹角 θ=600,物块与传送带间动摩擦因数为 μ=0.3,取 g=10m/s2,试求:
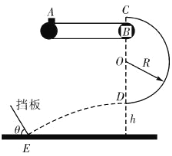
(1)小物块经过 D 点时的速度大小;
(2)传送带 A、B 间的最小距离 L
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)物块离开D点后平抛到恰好垂直到板上E点,则:h=![]() gt2 vy=gt
gt2 vy=gt
解得vy=![]() m/s;
m/s;
由![]()
解得vD=![]()
(2)小球从C点到D点,根据动能定理:![]()
小物块过C点恰能做圆周运动,在C点:mg=m![]()
则![]() 解得vC=3m/s;
解得vC=3m/s;
在传送带上:a=μg=3m/s2;
加速位移:![]() 则Lmin=1.5m
则Lmin=1.5m

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目