题目内容
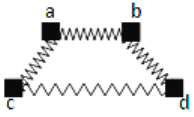
【题目】如图所示,AD与A1D1为水平放置的无限长平行金属导轨,DC与D1C1为倾角为![]() 的平行金属导轨,两组导轨的间距均为l=1.5m,导轨电阻忽略不计.质量为m1=0.35kg、电阻为R1=1
的平行金属导轨,两组导轨的间距均为l=1.5m,导轨电阻忽略不计.质量为m1=0.35kg、电阻为R1=1![]() 的导体棒ab置于倾斜导轨上,质量为m2=0.4kg、电阻为R2=0.5
的导体棒ab置于倾斜导轨上,质量为m2=0.4kg、电阻为R2=0.5![]() 的导体棒cd置于水平导轨上,轻质细绳跨过光滑滑轮一端与cd的中点相连、另一端悬挂一轻质挂钩.导体棒ab、cd与导轨间的动摩擦因数相同,且最大静摩擦力等于滑动摩擦力.整个装置处于竖直向上的匀强磁场中,磁感应强度为B=2T.初始时刻,棒ab在倾斜导轨上恰好不下滑.(g取10m/s2,sin
的导体棒cd置于水平导轨上,轻质细绳跨过光滑滑轮一端与cd的中点相连、另一端悬挂一轻质挂钩.导体棒ab、cd与导轨间的动摩擦因数相同,且最大静摩擦力等于滑动摩擦力.整个装置处于竖直向上的匀强磁场中,磁感应强度为B=2T.初始时刻,棒ab在倾斜导轨上恰好不下滑.(g取10m/s2,sin![]() =0.6)
=0.6)

(1)求导体棒与导轨间的动摩擦因数![]() ;
;
(2)在轻质挂钩上挂上物体P,细绳处于拉伸状态,将物体P与导体棒cd同时由静止释放,当P的质量不超过多大时,ab始终处于静止状态?(导体棒cd运动过程中,ab、cd一直与DD1平行,且没有与滑轮相碰.)
(3)若P的质量取第(2)问中的最大值,由静止释放开始计时,当t=1s时cd已经处于匀速直线运动状态,求在这1s内ab上产生的焦耳热为多少?
【答案】(1) ![]() (2)1.5kg (3)8.4J
(2)1.5kg (3)8.4J
【解析】(1)对ab棒,由平衡条件得![]()
解得![]() (或0.75)
(或0.75)
(2)当P的质量最大时,P和cd的运动达到稳定时,P和cd一起做匀速直线运动,ab处于静止状态,但摩擦力达到最大且沿斜面向下。设此时电路中的电流为I

对ab棒,由平衡条件得
沿斜面方向: ![]()
垂直于斜面方向: ![]()
或水平方向: ![]()
竖直方向: ![]()
对cd棒,设绳中的张力为T,由平衡条件得![]()
对P,由平衡条件得![]()
联立以上各式得: ![]()
故当P的质量不超过1.5Kg时,ab始终处于静止状态
(3)设P匀速运动的速度为v,由法拉第电磁感应定律和闭合电路欧姆定律得Blv=I(R1+R2)
得v=2m/s)
对P、棒cd,由牛顿第二定律得![]()
两边同时乘以![]() ,并累加求和,可得
,并累加求和,可得![]()
解得![]() m
m
对P、ab棒和cd棒,由能量守恒定律得![]() ,解得
,解得![]()
在这1s内ab棒上产生的焦耳热为![]()

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案