题目内容
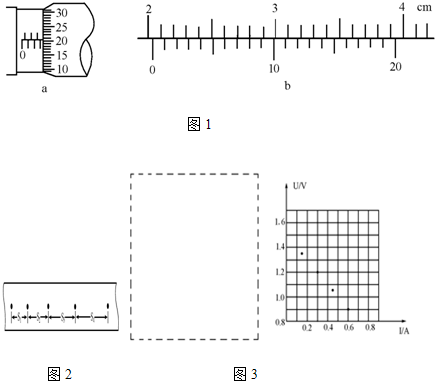
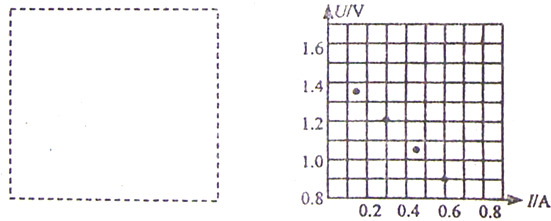
㈠(1)某学生用螺旋测微器在测定某一金属丝的直径时,测得的结果如下图1所示,则该金属丝的直径d=______mm.另一位学生用游标尺上标有20等分刻度的游标卡尺测一工件的长度,测得的结果如图所2示,则该工件的长度L=______cm.
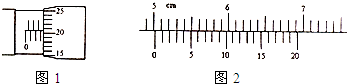
(2)如图3是某同学用打点计时器做的“研究小车的匀变速直线运动”实验时打出的一条纸带,A、B、C、D、E为该同学在纸带上选的计数点,相邻计数点间还有4个点未画出.
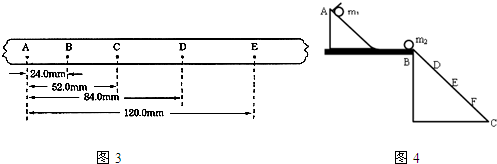
由图3可知:打点计时器打下D点时小车的瞬时速度为______m/s,小车的加速度为______ m/s2
㈡、为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同,质量不等的小球,按下述步骤做了如下实验:
①用天平测出两小球的质量分别为m1 和m2,且 m1>m2
②按照如图4所示的那样,安装好实验装置.将斜槽AB固定在桌边,使槽的末端点的切线水平.并与斜面BC连接在斜槽末端.
③先不放小球m2,让小球m1 从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置.
④将小球m2 放在斜槽前端边缘处,让小球m1从斜槽顶端A处滚下,使它们发生碰撞.记下小球m1和小球m2在斜面上的落点置.
⑤用毫米刻度尺量出各落点位置到斜槽末端点B的距离.图4中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD,LE,LF.
根据该同学的实验,回答下列问题:
(1)小球m1与m2发生碰撞后,m1的落点是图中的点______,m2的落点是图中的点______.
(2)用测得的物理量来表示,只要满足关系式______,则说明碰撞中动量是守恒的.
(3)用测得的物理量来表示,只要再满足关系式______,则说明两小球的碰撞时弹性碰撞.

(2)如图3是某同学用打点计时器做的“研究小车的匀变速直线运动”实验时打出的一条纸带,A、B、C、D、E为该同学在纸带上选的计数点,相邻计数点间还有4个点未画出.

由图3可知:打点计时器打下D点时小车的瞬时速度为______m/s,小车的加速度为______ m/s2
㈡、为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同,质量不等的小球,按下述步骤做了如下实验:
①用天平测出两小球的质量分别为m1 和m2,且 m1>m2
②按照如图4所示的那样,安装好实验装置.将斜槽AB固定在桌边,使槽的末端点的切线水平.并与斜面BC连接在斜槽末端.
③先不放小球m2,让小球m1 从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置.
④将小球m2 放在斜槽前端边缘处,让小球m1从斜槽顶端A处滚下,使它们发生碰撞.记下小球m1和小球m2在斜面上的落点置.
⑤用毫米刻度尺量出各落点位置到斜槽末端点B的距离.图4中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD,LE,LF.
根据该同学的实验,回答下列问题:
(1)小球m1与m2发生碰撞后,m1的落点是图中的点______,m2的落点是图中的点______.
(2)用测得的物理量来表示,只要满足关系式______,则说明碰撞中动量是守恒的.
(3)用测得的物理量来表示,只要再满足关系式______,则说明两小球的碰撞时弹性碰撞.
(一)(1)由图1所示螺旋测微器可知,螺旋测微器的固定刻度示数是3mm,
可动刻度示数是20.6×0.01mm=0.206mm,螺旋测微器的示数是3mm+0.206mm=3.206mm;
由图2所示游标卡尺可知,主尺示数是5cm,游标尺示数是3×0.05mm=0.15mm=0.015cm,
则游标卡尺的示数是5cm+0.015cm=5.015cm.
(2)由图3可知:sCE=sAE-sAC=120.0mm-52.0mm=68mm=0.068m,
则在D点时小车的瞬时速度vD=
=
=0.34m/s;
由图3可知:sDE=sAE-sAD=120.0mm-84.0mm=36mm=0.036m,
sCD=sAD-sAC=84.0mm-52.0mm=32.0mm=0.032m,
小车的加速度a=
=
=0.4m/s2;
(二)(1)m1与m2相撞后,m2的速度增大,m1的速度减小,m1的速度小于m2的速度,它们都做平抛运动,
m1的水平位移小于m2的水平位移,因此E点是碰前m1的落地点,D是碰后m1的落地点,F是碰后m2的落地点.
(2)设斜面BC的倾角是θ,小球离开斜槽AB后做平抛运动;
碰前小球m1的落地点是E,它的水平位移x1=LEcosθ=v1t1,
竖直位移y1=LEsinθ=
gt12,解得v1=LEcosθ
;
碰后小球m1的落地点是D,它的水平位移x1′=LDcosθ=v1′t1′,
竖直位移y1′=LD′sinθ=
gt12,解得v1′=LDcosθ
;
碰后小球m2的落地点是F,它的水平位移x2=LFcosθ=v2t2,
竖直位移y2′=LFsinθ=
gt2′2,解得v2′=LFcosθ
;
如果m1v1=m1v1′+m2v2′,m1LEcosθ
=m1LDcosθ
+m2LFcosθ
,
即当m1
=m1
+m2
时,说明碰撞中动量是守恒的.
如果
m1v12=
m1v1′2+
m2v2′2,即当m1LE=m1LD+m2LF时,说明两小球的碰撞时弹性碰撞.
故答案为:(一)(1)3.206;5.015;(2)0.34;0.4;
(二)(1)D;F;(2)m1
=m1
+m2
;(3)m1LE=m1LD+m2LF.
可动刻度示数是20.6×0.01mm=0.206mm,螺旋测微器的示数是3mm+0.206mm=3.206mm;
由图2所示游标卡尺可知,主尺示数是5cm,游标尺示数是3×0.05mm=0.15mm=0.015cm,
则游标卡尺的示数是5cm+0.015cm=5.015cm.
(2)由图3可知:sCE=sAE-sAC=120.0mm-52.0mm=68mm=0.068m,
则在D点时小车的瞬时速度vD=
| sCE |
| tCE |
| 0.068m |
| 0.1s×2 |
由图3可知:sDE=sAE-sAD=120.0mm-84.0mm=36mm=0.036m,
sCD=sAD-sAC=84.0mm-52.0mm=32.0mm=0.032m,
小车的加速度a=
| sDE-sCD |
| t2 |
| 0.036m-0.032m |
| (0.1s)2 |
(二)(1)m1与m2相撞后,m2的速度增大,m1的速度减小,m1的速度小于m2的速度,它们都做平抛运动,
m1的水平位移小于m2的水平位移,因此E点是碰前m1的落地点,D是碰后m1的落地点,F是碰后m2的落地点.
(2)设斜面BC的倾角是θ,小球离开斜槽AB后做平抛运动;
碰前小球m1的落地点是E,它的水平位移x1=LEcosθ=v1t1,
竖直位移y1=LEsinθ=
| 1 |
| 2 |
|
碰后小球m1的落地点是D,它的水平位移x1′=LDcosθ=v1′t1′,
竖直位移y1′=LD′sinθ=
| 1 |
| 2 |
|
碰后小球m2的落地点是F,它的水平位移x2=LFcosθ=v2t2,
竖直位移y2′=LFsinθ=
| 1 |
| 2 |
|
如果m1v1=m1v1′+m2v2′,m1LEcosθ
|
|
|
即当m1
| LE |
| LD |
| LF |
如果
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(一)(1)3.206;5.015;(2)0.34;0.4;
(二)(1)D;F;(2)m1
| LE |
| LD |
| LF |

练习册系列答案
相关题目