题目内容
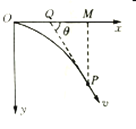
【题目】如图所示,足够长的粗糙绝缘斜面与水平面成θ=37°放置,在斜面上直线aa′和bb′与斜面底边平行,在aa′,bb′围成的区域有垂直斜面向上的有界匀强磁场,磁感应强度为B=l T;现有一质量为m=10 g,总电阻R=1Ω.边长d=0.1 m的正方形金属线圈MNQP,让PQ边与斜面底边平行,从斜面上端静止释放,线圈刚好匀速穿过整个磁场区域,已知线圈与斜面间的动摩擦因数为μ=0.5,( g= 10 m/s2,sin 37°=0.6,cos 37°=0.8)求:

(1)线圈进入磁场区域时的速度;
(2)线圈释放时,PQ边到bb′的距离;
(3)整个线圈穿过磁场的过程中,线圈上产生的焦耳热。
【答案】(1) 2m/s (2) 1m (3) 4×10-3J
【解析】
(1) 设线圈匀速进入磁场时的速度为v,对线圈受力分析,得:
FA+μmgcosθ=mgsinθ
而
FA=BId,![]() ,E=Bdv
,E=Bdv
联立解得:
v=2m/s
(2) 设PQ边到bb′的距离为L,根据动能定理:
![]()
解得:
L=1m
(3) 由于线圈刚好匀速穿过整个磁场区域,则磁场宽度等于线圈边长d,则线圈进入磁场到离开磁场,经过的路程为2d,则有:
Q=FA2d=(0.02×0.2)J=4×10-3J

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目