Question

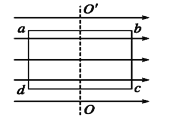
【题目】如图所示，一斜面体固定在水平地面上，倾角为θ=30°、高度为h=1.6m。一薄木板B置于斜面顶端，恰好能保持静止，木板下端连接有一根自然长度为l0=0.2m的轻弹簧，木板总质量为m=1kg，总长度为L=2.0m。一质量为M=3kg的小物块A从斜面体左侧某位置水平抛出，物块A经过一段时间后从斜面顶端以4m/s的速率沿平行于斜面方向落到木板B上并开始向下滑行，已知A、B之间的动摩擦因数为。木板下滑到斜面底端碰到挡板时立刻停下，物块A最后恰好能脱离弹簧，且弹簧被压缩时一直处于弹性限度内，最大静摩擦力等于滑动摩擦力，取重力加速度g=10m/s2，不计空气阻力。求：

(1)物体A水平抛出时离地面的高度H；

(2)薄木板B从开始运动到与档板碰撞所需的时间；

(3)弹簧被压缩到最短时的弹性势能。

Answer 1

【答案】(1)1.8m；(2)0.6s；(3)5J

【解析】

(1)物块A落到B上时

解得

vy＝2m/s

物块A落到木板前做平抛运动，竖直方向：

解得

H＝1.8m

(2)由木板恰好静止在斜面上，得到斜面与木板间的动摩擦因数μ0应满足：

mgsin 30°＝μ0mgcos 30°

得

物块A在木板上滑行时，以A为研究对象有：

(沿斜面向上)

以木板B为研究对象有：

(沿斜面向下)

假设A与木板达到共同速度v共时，A还没有压缩弹簧且木板还没有到达底端，则有：

v共＝aBt1＝v－aAt1

解得

v共＝3 m/s，t1＝0.4 s

此过程

故

Δx＝xA－xB＝0.8 m<L－l0＝1.8m

说明以上假设成立

共速后，由于(M＋m)gsin 30°＝μ0(M＋m)gcos 30°，A与木板B一起匀速到木板与底端挡板碰撞，该过程所需时间

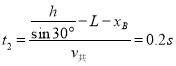
所以

t=t1+t2=0.6s

(3)木板停下，此后A做匀减速到与弹簧接触，然后A压缩弹簧至最短，设接触弹簧时A的速度为vA，有：

－2aA(L－l0－Δx)＝vA2－v共2

解得

vA＝2 m/s

设弹簧最大压缩量为xm，A从开始压缩弹簧到刚好回到原长过程有：

Q＝2μMgxmcos 30°＝

得

Q＝6 J，xm＝m

A从开始压缩弹簧到弹簧最短过程有

Epm＝＋Mgxmsin 30°－＝5 J

即弹簧被压缩到最短时的弹性势能为5J。