题目内容
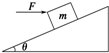质量为m的物体放在倾角为θ的斜面上，它跟斜面间的动摩擦因数为μ．在水平恒力F作用下，物体沿斜面匀速向上运动，如图所示．物体受到的摩擦力可表示为（ ）| A、μmgsinθ | B、μ（mgcosθ+Fsinθ） | C、Fcosθ-mgsinθ | D、μ（mgcosθ-Fsinθ） |
分析：对物体受力分析，物体受重力，推力，斜面的支持力，摩擦力．由物体处于平衡状态，可以由正交分解求出物体所受的摩擦力．
解答：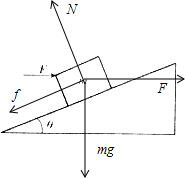
解：物体受力如图：
由正交分解可知，在运动方向上有：
f+mgsinθ=Fcosθ
解得：f=Fcosθ-mgsinθ
在垂直于运动方向上有：N=mgcosθ+Fsinθ
又：f=μN
解得：f=μ（mgcosθ+Fsinθ）
故选：BC
解：物体受力如图：由正交分解可知，在运动方向上有：
f+mgsinθ=Fcosθ
解得：f=Fcosθ-mgsinθ
在垂直于运动方向上有：N=mgcosθ+Fsinθ
又：f=μN
解得：f=μ（mgcosθ+Fsinθ）
故选：BC
点评：本题设计摩擦力的结果，由两种方式，一是有受力平衡得到的结果，二是由定义式得到的结果，摩擦力会有两个表达式，做题时应全部做出来．
练习册系列答案
相关题目
如图所示，一个质量为m的物体放在倾角为α的粗糙斜面上，保持静止，现用水平力F推物体，当F由零增加稍许，而物体仍保持静止，则（ ）
如图所示，质量为m的物体放在倾角为θ的斜面上，它跟斜面的动摩擦因数为μ，在水平恒力F的作用下，物体沿斜面匀速向上运动．则物体所受摩擦力大小是（ ）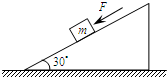
如图所示，质量为m的物体放在倾角为30°的斜面上，在平行斜面向下的力F作用下处于静止状态，下列关于斜面对物体摩擦力大小的说法，正确的是（ ）