��Ŀ����
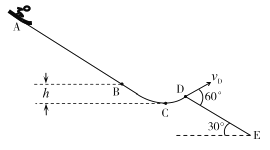
����Ŀ����ͼ��ʾ���⻬��Ե�İ�Բ�ι���̶�����ֱƽ���ڣ���Բ�ι����⻬��Ե��ˮƽ���������ڰ�Բ�Ķ˵�A��һ����Ϊ1kg��С����ˮƽ�����������˶����ٶ�Ϊv=6m/s����A�˶��������ߵ�B�����������ˮƽ�����ϵ�D�㣨ͼ��δ����������֪�����ռ������ֱ���µ���ǿ�糡��С�������ɣ�С�����ܵ糡���Ĵ�С����![]() ��gΪ�������ٶȣ�
��gΪ�������ٶȣ�
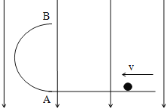
(1)������뾶R=0.1mʱ����С���Բ�ι��B��ʱ�Թ����ѹ����
(2)ΪʹС�����˶��������ߵ�B�������뾶�����ֵ��
���𰸡�(1)![]() ��������ֱ���ϣ�(2)0.24m
��������ֱ���ϣ�(2)0.24m
��������
(1)��С��Բ���![]() ��ʱ�ٶ�Ϊ
��ʱ�ٶ�Ϊ![]() ����
����![]() ��
��![]() �Ĺ����������͵糡���������ɶ��ܶ����У�
�Ĺ����������͵糡���������ɶ��ܶ����У�
![]()
��ã�
![]()
��ţ�ٵڶ������У�
![]()
�������ݽ�ã�
![]()
ţ�ٵ������ɿ�֪��С��Բ���![]() ��ʱ�Թ����ѹ��Ϊ��
��ʱ�Թ����ѹ��Ϊ��
![]()
������ֱ����
(2)����뾶Խ��С����ߵ���ٶ�ԽС����С��ǡ�õ�����ߵ�ʱ�������С���������Ϊ�㣬��С��Թ����ѹ��ҲΪ�㣬��ʱ����뾶�����
![]()
�ɶ��ܶ����У�
![]()
�������ݽ�ù���뾶�����ֵ��
![]()

��ϰ��ϵ�д�
�����Ŀ