题目内容
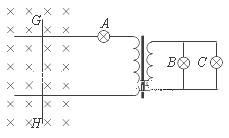
【题目】如图所示，水平轨道与半径为
的半圆弧形轨道平滑连接于S点，两者均光滑且绝缘，并安装在固定的竖直绝缘平板上。在竖直平板上、下侧面各有一块正对水平金属板
，两板间距为
，半圆轨道的最高点
、最低点
及板右侧边缘点在同一竖直线上。装置左侧有一半径为
的水平金属圆环，圆环平面区域内存在竖直向下的、磁感应强度大小为
的匀强磁场，一根长度略大于的金属杆一端置于圆环上，另一端与过圆心
的竖直的转轴连接，转轴带动金属杆转动，在圆环边缘和转轴处引出导线分别与连接，图中电阻阻值为
，不计其它电阻。右侧水平轨道上有一带电量为
、质量为
的小球1以速度
向左运动，与水平轨道上静止的、质量也为的不带电小球2发生碰撞后，粘合在一起共同向左运动，小球及粘合体均看作质点，碰撞过程没有电荷损失。设板间正对区域才存在电场，重力加速度为
。
（1）求小球1与2碰撞后粘合体的速度大小
；
（2）若金属杆转动的角速度为
，求定值电阻消耗的电功率
;
（3）要使两球碰后的粘合体能从半圆轨道的最低点做圆周运动到最高点，且粘合体恰能过最高点，求金属杆转动的角速度.
【答案】（1）
（2）
（3）
【解析】
（1）1、2碰：
得：
（2）
得：
（3）电场力
设等效重力加速度为
则
即
因 
得：
练习册系列答案
阅读快车系列答案
相关题目
