Question

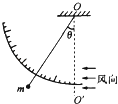
【题目】一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端，如图，斜面静止时，球紧靠在斜面上，绳与斜面平行，不计摩擦，当斜面以10m/s2的加速度向右做加速运动时，则（ ）（sin53°=0.8，cos53°=0.6，g=10m/s2 ）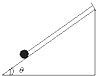

A.绳的拉力为1.60N
B.绳的拉力为2 N
C.斜面对小球的弹力为1.20N
D.斜面对小球的弹力为0

Answer 1

【答案】B,D
【解析】解：当加速度a较小时，小球与斜面一起运动，此时小球受重力、绳子拉力和斜面的支持力，绳子平行于斜面；当加速度a足够大时，小球将飞离斜面，此时小球仅受重力与绳子的拉力作用，绳子与水平方向的夹角未知，而题目要求出当斜面以10m/s2的加速度向右做加速运动时，绳的拉力及斜面对小球的弹力，必须先求出小球离开斜面的临界加速度a0，（此时小球所受斜面的支持力恰好为零）

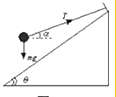
小球的受力如图：

由牛顿第二定律得：F合=mgcotθ=ma0

解得：a0=gcotθ=7.5m/s2

因为：a=10m/s2＞a0

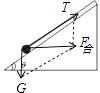
所以小球一定离开斜面N=0，小球的受力如图所示：

则水平方向有牛顿第二定律得：Tcosα=ma

竖直方向有受力平衡得：Tsinα=mg

由以上两式整理得：T= = =2 N；

N=0
故AC不符合题意，B的符合题意；

所以答案是：BD．

【考点精析】利用力的合成和力的分解对题目进行判断即可得到答案，需要熟知求几个已知力的合力，叫做力的合成；共点的两个力（F 1 和F 2 ）合力大小F的取值范围为:|F 1 -F 2 |≤F≤F 1 +F 2；求一个已知力的分力，叫做力的分解（力的分解与力的合成互为逆运算）；在实际问题中，通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究，在很多问题中都采用正交分解法．