题目内容
15.在圆形轨道上匀速运行的质量为m的人造地球卫星,它到地面的距离等于地球的半径R,地面上的重力加速度为g,求:卫星的运行周期.分析 人造地球卫星绕地球做匀速圆周运动,地球对人造卫星的万有引力提供向心力,根据牛顿第二定律可列式求出周期和向心力的表达式.再根据万有引力近似等于重力得出黄金代换公式即可.
解答 解:人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设地球质量为M、卫星的轨道半径为r,
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
r=2R
忽略地球自转的影响有 $\frac{GMm}{{R}^{2}}$=mg
解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$=4π$\sqrt{\frac{2R}{g}}$
答:卫星的运行周期是4π$\sqrt{\frac{2R}{g}}$.
点评 本题关键根据人造卫星的万有引力充当向心力,以及地球表面物体的重力等于万有引力列两个方程求解.

练习册系列答案
相关题目
10.两个物体的质量分别是M1和M2,当它们的距离为R时,两物体间的万有引力为F.若将它们的距离减为原来的一半时(两物体仍可视为质点),则两物体间的万有引力变为( )
| A. | $\frac{1}{2}$F | B. | $\frac{1}{4}$F | C. | 2F | D. | 4F |
20. 如图所示,一个小的光源S发出白光,经三棱镜分光.若人沿着折射光线的反方向观察,通过棱镜可以看到( )
如图所示,一个小的光源S发出白光,经三棱镜分光.若人沿着折射光线的反方向观察,通过棱镜可以看到( )
 如图所示,一个小的光源S发出白光,经三棱镜分光.若人沿着折射光线的反方向观察,通过棱镜可以看到( )
如图所示,一个小的光源S发出白光,经三棱镜分光.若人沿着折射光线的反方向观察,通过棱镜可以看到( )| A. | 白光点 | B. | 光点上部红色,下部紫色 | ||
| C. | 光点上部紫色,下部红色 | D. | 看不到光源的像 |
7. 足球被斜向上踢出时的速度大小为v,方向与水平方向成α角,把这个速度沿水平和竖直方向分解,其水平分速度的大小是( )
足球被斜向上踢出时的速度大小为v,方向与水平方向成α角,把这个速度沿水平和竖直方向分解,其水平分速度的大小是( )
 足球被斜向上踢出时的速度大小为v,方向与水平方向成α角,把这个速度沿水平和竖直方向分解,其水平分速度的大小是( )
足球被斜向上踢出时的速度大小为v,方向与水平方向成α角,把这个速度沿水平和竖直方向分解,其水平分速度的大小是( )| A. | vsinα | B. | vcosα | C. | $\frac{v}{sinα}$ | D. | $\frac{v}{cosα}$ |
5. 如图所示,两个相等的轻质铝环套在一根水平光滑绝缘杆上,当一条形磁铁向左运动靠近两环时,两环的运动情况是( )
如图所示,两个相等的轻质铝环套在一根水平光滑绝缘杆上,当一条形磁铁向左运动靠近两环时,两环的运动情况是( )
 如图所示,两个相等的轻质铝环套在一根水平光滑绝缘杆上,当一条形磁铁向左运动靠近两环时,两环的运动情况是( )
如图所示,两个相等的轻质铝环套在一根水平光滑绝缘杆上,当一条形磁铁向左运动靠近两环时,两环的运动情况是( )| A. | 同时向左运动,间距变大 | B. | 同时向左运动,间距变小 | ||
| C. | 同时向右运动,间距变小 | D. | 同时向右运动,间距变大 |
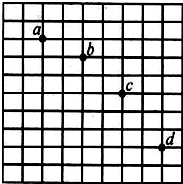 在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=6.4cm,若小球在平抛运动途中的几个位置如图a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gL}$(用L、g表示),其值是1.6 m/s(取g=10m/s2);b点的速度vb=$\frac{5}{2}\sqrt{gL}$(用L、g表示).
在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=6.4cm,若小球在平抛运动途中的几个位置如图a、b、c、d所示,则小球平抛的初速度的计算式为v0=2$\sqrt{gL}$(用L、g表示),其值是1.6 m/s(取g=10m/s2);b点的速度vb=$\frac{5}{2}\sqrt{gL}$(用L、g表示). 如图所示,质量为M的足够长木板置于光滑水平地面上,一质量为m的木块以水平初速度v0滑上长木板,已知木块与木板之间的摩擦因数为μ,求:
如图所示,质量为M的足够长木板置于光滑水平地面上,一质量为m的木块以水平初速度v0滑上长木板,已知木块与木板之间的摩擦因数为μ,求: