题目内容
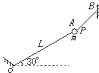 如图所示,用长为L不可伸长的细线连结质量为m的小球,绳的O端固定,另用细线AB将小球拉起使细线OA与水平成30°角.现将AB线从A处剪断.求?
如图所示,用长为L不可伸长的细线连结质量为m的小球,绳的O端固定,另用细线AB将小球拉起使细线OA与水平成30°角.现将AB线从A处剪断.求?(1)剪断细线AB的瞬间小球的加速度;?
(2)剪断细线AB后小球落到最低点时细线L中的张力.
分析:(1)剪断细线AB的瞬间,细线L的拉力立即消失,小球只受重力,根据牛顿第二定律求得加速度;
(2)剪断细线AB后小球先自由下落,当绳子绷紧后,沿绳子方向的分速度突然消失,只有切向分速度,以此速度再继续做圆周运动.先根据机械能守恒定律求得绳子刚绷紧瞬间小球的速度,再将速度分解得到切向速度,即为圆周运动的初速度,再根据机械能守恒列式,求出小球到达最低点时的速度.在最低点,由重力和拉力的合力提供小球的向心力,由牛顿第二定律求解.
(2)剪断细线AB后小球先自由下落,当绳子绷紧后,沿绳子方向的分速度突然消失,只有切向分速度,以此速度再继续做圆周运动.先根据机械能守恒定律求得绳子刚绷紧瞬间小球的速度,再将速度分解得到切向速度,即为圆周运动的初速度,再根据机械能守恒列式,求出小球到达最低点时的速度.在最低点,由重力和拉力的合力提供小球的向心力,由牛顿第二定律求解.
解答:解:(1)剪断细线AB后,细线L中的拉力立即消失,小球只受重力作用,小球加速度为g,方向竖直向下.?
(2)剪断细线AB后,小球在PQ之间自由下落,当绳L再次与水平方向成30°角时将被张紧,设绳张紧前速度为v1.?
由机械能守恒定律得:2mgLsin30°=
mv12?
得:v1=
小球的切向速度为:vt=v1cos30°=
设小球到达最低点的速度大小为v2.
由Q到最低点的过程中机械能守恒,有:
mv22=
mvt2+mgL(1-sin30°)?
在最低点时,小球所受的合力提供向心力,由牛顿第二定律有:
T-mg=m
联立上述各式得:T=
mg?
答:(1)剪断细线AB的瞬间小球的加速度为g;?
(2)剪断细线AB后小球落到最低点时细线L中的张力为
mg.
(2)剪断细线AB后,小球在PQ之间自由下落,当绳L再次与水平方向成30°角时将被张紧,设绳张紧前速度为v1.?
由机械能守恒定律得:2mgLsin30°=
| 1 |
| 2 |
得:v1=
| 2gL |
小球的切向速度为:vt=v1cos30°=
| ||
| 2 |
设小球到达最低点的速度大小为v2.
由Q到最低点的过程中机械能守恒,有:
| 1 |
| 2 |
| 1 |
| 2 |
在最低点时,小球所受的合力提供向心力,由牛顿第二定律有:
T-mg=m
| ||
| L |
联立上述各式得:T=
| 3 |
| 2 |
答:(1)剪断细线AB的瞬间小球的加速度为g;?
(2)剪断细线AB后小球落到最低点时细线L中的张力为
| 3 |
| 2 |
点评:本题容易出错之处是绳子绷紧瞬间速度会突变,学生往往不知道,要注意中学物理中绳子是理想化的模型,伸长不计,弹力可以突变.

练习册系列答案
相关题目
 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )| A、小球在圆周最高点时所受的向心力一定为重力 | ||
| B、小球在最高点时绳子的拉力不可能为零 | ||
C、若小球刚好能在竖直平面内做圆周运动,则其在最高点的速率为
| ||
| D、小球过最低点时绳子的拉力不一定大于小球重力 |
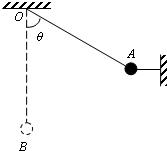 如图所示,用长为L的细线OA和水平细线将质量为m的小球系住,此时细线OA与竖直方向成θ=
如图所示,用长为L的细线OA和水平细线将质量为m的小球系住,此时细线OA与竖直方向成θ= 如图所示,用长为l的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )
如图所示,用长为l的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( ) 如图所示,用长为L且不可伸长的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )
如图所示,用长为L且不可伸长的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法中正确的是( )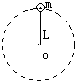 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法正确的是( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做圆周运动,则下列说法正确的是( )