题目内容
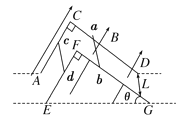
【题目】如图所示,ACD、EFG为两根相距L的足够长的金属直角导轨,它们被竖直固定在绝缘水平面上,CDGF面与水平面成θ角。两导轨所在空间存在垂直于CDGF平面向上的匀强磁场,磁感应强度大小为B。两根质量均为m、长度均为L的金属细杆ab、cd与导轨垂直接触形成闭合回路,杆与导轨之间的动摩擦因数均为![]() ,两金属细杆的电阻均为R,导轨电阻不计。当ab以速度v1沿导轨向下匀速运动时,cd杆也正好以速度v2向下匀速运动,重力加速度为g。以下说法正确的是( )
,两金属细杆的电阻均为R,导轨电阻不计。当ab以速度v1沿导轨向下匀速运动时,cd杆也正好以速度v2向下匀速运动,重力加速度为g。以下说法正确的是( )
A.回路中的电流强度为![]()
B.ab杆所受摩擦力为mgsinθ
C.cd杆所受摩擦力为![]()
D.μ与v1大小的关系为μ=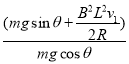
【答案】C
【解析】
A.cd棒不切割磁感线,ab杆产生的感应电动势 E=BLv1,回路中感应电流
I=![]() =
=![]()
故A错误;
B.ab杆匀速下滑,受力平衡条件,则ab杆所受的安培力大小为
F安=BIL=![]()
方向沿轨道向上,则由平衡条件,ab所受的摩擦力大小为
f=mgsin![]() -F安= mgsin
-F安= mgsin![]() -
-![]()
故B错误;
C.cd杆所受的安培力大小也等于F安,方向垂直于导轨向下,则cd杆所受摩擦力为
f=![]() FN=
FN=![]() [mgcos(90
[mgcos(90![]() -
-![]() )+F安]=
)+F安]=![]()
故C正确;
D.根据cd杆受力平衡得
mgsin(90°-![]() )=
)=![]()
则得![]() 与v1大小的关系
与v1大小的关系
![]() =
=
故D错误。

练习册系列答案
相关题目