题目内容
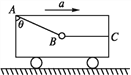
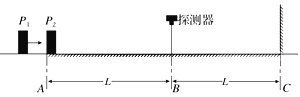
【题目】如图的水平轨道中，AC段的中点B的正上方有一探测器，C处有一竖直挡板，物体P1沿轨道向右以速度v1与静止在A点的物体P2碰撞，并接合成复合体P，以此碰撞时刻为计时零点，探测器只在t1=2 s至t2=4 s内工作，已知P1、P2的质量都为m=1 kg，P与AC间的动摩擦因数为μ=0.1，AB段长L=4 m，g取10 m/s2，P1、P2和P均视为质点，P与挡板的碰撞为弹性碰撞。
(1)若v1=6 m/s，求P1、P2碰后瞬间的速度大小v和碰撞损失的动能ΔE；
(2)若P与挡板碰后，能在探测器的工作时间内通过B点，求v1的取值范围和P向左经过A点时的最大动能E。
【答案】（1）9J （2）10m/s＜v1＜14m/s 17J
【解析】试题分析：（1）由于P1和P2发生弹性碰撞，据动量守恒定律有：
碰撞过程中损失的动能为：
（2）
解法一：根据牛顿第二定律，P做匀减速直线运动，加速度a=
设P1、P2碰撞后的共同速度为vA，则根据（1）问可得vA=v1/2
把P与挡板碰撞前后过程当作整体过程处理
经过时间t1，P运动过的路程为s1，则
经过时间t2，P运动过的路程为s2，则
如果P能在探测器工作时间内通过B点，必须满足s1≤3L≤s2
联立以上各式，解得10m/s＜v1＜14m/s
v1的最大值为14m/s，此时碰撞后的结合体P有最大速度vA=7m/s
根据动能定理，
代入数据，解得E=17J
解法二：从A点滑动到C点，再从C点滑动到A点的整个过程，P做的是匀减速直线。
设加速度大小为a，则a=μg=1m/s2
设经过时间t，P与挡板碰撞后经过B点，[则：
vB=v-at，
，v=v1/2
若t=2s时经过B点，可得v1="14m/s"
若t=4s时经过B点，可得v1=10m/s
则v1的取值范围为：10m/s＜v1＜14m/s
v1=14m/s时，碰撞后的结合体P的最大速度为：
根据动能定理，
代入数据，可得通过A点时的最大动能为：
