题目内容
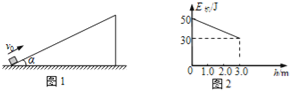
【题目】如图1所示,物体以一定初速度从倾角α=37°的斜面底端沿斜面向上运动,上升的最大高度为3.0m.选择地面为参考平面,上升过程中,物体的机械能E机随高度h的变化如图2所示.g=10m/s2,sin37°=0.60,cos37°=0.80.则( )
A. 物体的质量m=0.67kg
B. 物体与斜面间的动摩擦因数μ=0.40
C. 物体上升过程的加速度大小a=10m/s2
D. 物体回到斜面底端时的动能Ek=10J
【答案】CD
【解析】试题分析:当物体到达最高点时速度为零,机械能等于物体的重力势能,由重力势能计算公式可以求出物体质量;
在整个运动过程中,机械能的变化量等于摩擦力做的功,由图象求出摩擦力的功,由功计算公式求出动摩擦因数;
由牛顿第二定律求出物体上升过程的加速度;由动能定理求出物体回到斜面底端时的动能.
解:A、物体到达最高点时,机械能E=EP=mgh,m=![]() =
=![]() =1kg,故A错误;
=1kg,故A错误;
B、物体上升过程中,克服摩擦力做功,机械能减少,减少的机械能等于克服摩擦力的功,
△E=﹣μmgcosα![]() ,即30﹣50=﹣μ×1×10cos37°×
,即30﹣50=﹣μ×1×10cos37°×![]() ,μ=0.5,故B错误;
,μ=0.5,故B错误;
C、物体上升过程中,由牛顿第二定律得:mgsinα+μmgcosα=ma,解得a=10m/s2,故C正确;
D、由图象可知,物体上升过程中摩擦力做功W=30﹣50=﹣20J,在整个过程中由动能定理得EK﹣EK0=2W,
则EK=EK0+2W=50+2×(﹣20)=10J,故D正确;
故选CD.

练习册系列答案
相关题目