题目内容
(12分)如图所示,起重机将重物吊运到高处的过程中经过A、B两点,重物的质量m="500" kg,A、B间的水平距离d ="10" m.重物自A点起,沿水平方向做v="1.0" m/s的匀速运动,同时沿竖直方向做初速度为零、加速度a=" 0.2" m/s2的匀加速运动,忽略吊绳的质量及空气阻力,取重力加速度g=" 10" m/s2.求:

(1)定性画出重物由A到B的运动轨迹;
(2)重物由A运动到B的时间;
(3)重物经过B点时速度的大小;
(4)由A到B的过程中,吊绳对重物所做的功.

(1)定性画出重物由A到B的运动轨迹;
(2)重物由A运动到B的时间;
(3)重物经过B点时速度的大小;
(4)由A到B的过程中,吊绳对重物所做的功.
(1)向上弯曲的抛物线 (2)10s (3)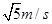 (4)51000J
(4)51000J
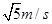 (4)51000J
(4)51000J试题分析:(1)由题意知水平方向做v="1.0" m/s的匀速运动,同时沿竖直方向做初速度为零、加速度a=" 0.2" m/s2的匀加速运动,所以轨迹为向上弯曲的抛物线 (2分)
(2)根据水平方向做匀速直线运动的:t=d/v=10s (2分)
(3)在竖直方向:v竖=at=2m/s (2分)
所以在B点的速度:
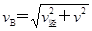 =
= 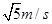 (2分)
(2分)(4)根据能量守恒可得:W=mgh+
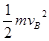 -
-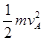 =51000J(或先求绳中的张力,再求张力的功) (4分)
=51000J(或先求绳中的张力,再求张力的功) (4分)
练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目









 的半球顶端,若此时小球的初速为
的半球顶端,若此时小球的初速为 时,物块对球顶恰无压力,则以下说法不正确的是:
时,物块对球顶恰无压力,则以下说法不正确的是:


 角
角
