题目内容
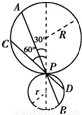如图所示，AB和CD是两条光滑斜槽，它们各自的两端分别位于半径为R和r的两个相切的竖直圆上，并且斜槽都通过切点P，有一个小球由静止分别从A滑到B和从C滑到D，所用的时间分别为t1和t2，则t1和t2之比为（ ）A．1：1
B．1：2
C．
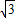：1D．1：
【答案】分析：对物体受力分析可知，小球在两条斜槽上的运动规律是一样的，只是加速度的大小和位移的大小不一样，由牛顿第二定律和匀变速直线运动的规律可以求得它们各自的运动时间．
解答：解：对物体受力分析可知：
当重物从A点下落时，重物受重力mg，支持力F，
在沿斜面方向上加速度是a1，重力分解：
mgcos30°=ma1，
解得 a1=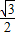
g，
根据公式：S=
a1t12，
得 S=2R×cos30°+2r×cos30°=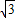
（R+r）
所以：t1=2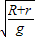
，
当重物从C点下滑时，受重力mg，支持力F，
在沿斜面方向上加速度是a2，重力分解：
mgcos60°=ma2，
解得 a2=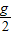
，
根据公式：S=
a2t22，
得S=2R×cos60°+2r×cos60°=R+r
t2=2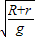
，
所以t1=t2 ，
故选：A．
点评：对于两种不同的情况，位移有大有小，它们之间的运动时间是什么关系？不能简单的从位移的大小上来看，要注意用所学的物理规律来推导．
解答：解：对物体受力分析可知：
当重物从A点下落时，重物受重力mg，支持力F，
在沿斜面方向上加速度是a1，重力分解：
mgcos30°=ma1，
解得 a1=
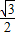g，根据公式：S=
a1t12，得 S=2R×cos30°+2r×cos30°=
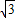（R+r）所以：t1=2
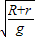，当重物从C点下滑时，受重力mg，支持力F，
在沿斜面方向上加速度是a2，重力分解：
mgcos60°=ma2，
解得 a2=
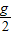，根据公式：S=
a2t22，得S=2R×cos60°+2r×cos60°=R+r
t2=2
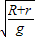，所以t1=t2 ，
故选：A．
点评：对于两种不同的情况，位移有大有小，它们之间的运动时间是什么关系？不能简单的从位移的大小上来看，要注意用所学的物理规律来推导．
练习册系列答案
相关题目
如图所示，AB和CD是足够长的平行光滑导轨，其间距为L，导轨平面与水平面的夹角为θ．整个装置处在磁感应强度为B，方向垂直于导轨平面向上的匀强磁场中，．AC端连有电阻值为R的电阻．若将一质量为M、电阻为r的金属棒EF垂直于导轨在距BD端s处由静止释放，在棒EF滑至底端前会有加速和匀速两个运动阶段．今用大小为F，方向沿斜面向上的恒力把棒EF从BD位置由静止推至距BD端s处，突然撤去恒力F，棒EF最后又回到BD端．（导轨的电阻不计）
如图所示，ab和cd是足够长的平行光滑导轨，其间距为l，导轨平面与水平面的夹角为θ．整个装置处在磁感应强度为B、方向垂直斜面向上的匀强磁场中．ac端连有电阻值为R的电阻．若将一质量为m，垂直于导轨的金属棒EF在距bd端S处由静止释放，在EF棒滑至底端前会有加速和匀速两个运动阶段．今用大小为F，方向沿斜面向上的恒力把EF棒从bd位置由静止推至距bd端S处，突然撤去恒力F，棒EF最后又回到bd端．已知金属棒EF的电阻为r，导轨的电阻不计，求：
如图所示，AB和CD是足够长的平行光滑导轨，其间距为L，导轨平面与水平面的夹角为α．整个装置处在磁感应强度为B、方向垂直于导轨平面且向上的匀强磁场中．AC端连有阻值为R的电阻．若将一质量为m、垂直于导轨的金属棒EF在距BD端s处由静止释放，则棒滑至底端前会有加速和匀速两个运动阶段（金属棒及导轨的电阻不计）．求：
如图所示，ab和cd是匀强磁场中与磁场方向垂直的平面内两条平行直线．在直线ab上的O点将同种带电粒子以不同的初速度发射出去，初速度方向均沿Ob方向．其中粒子1在通过直线cd时，速度为v1，方向与cd垂直；粒子2在通过直线cd时，速度为v2，方向与cd夹角为60°．从射出到经过直线cd，粒子1经历时间为t1，粒子2经历的时间为t2，则t1与t2的比值是（ ）
如图所示，AB和CD是半径为R=1m的