题目内容
如图所示,一条长为L的细线,上端固定,下端拴一质量为m的带电小球。将它置于一匀强电场中,电场强度大小为E,方向是水平的,已知当细线离开竖直的位置偏角为α时,小球处于平衡,问:
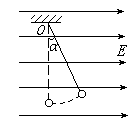
(1)小球带何种电荷?求小球所带电量。
(2)如果细线的偏角由α增大到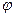 ,然后将小球由静止开始释放,则
,然后将小球由静止开始释放,则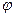 应多大,才能使在细线到竖直位置时,小球的速度刚好为零。
应多大,才能使在细线到竖直位置时,小球的速度刚好为零。

(1)小球带何种电荷?求小球所带电量。
(2)如果细线的偏角由α增大到
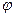 ,然后将小球由静止开始释放,则
,然后将小球由静止开始释放,则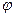 应多大,才能使在细线到竖直位置时,小球的速度刚好为零。
应多大,才能使在细线到竖直位置时,小球的速度刚好为零。(1)正电荷, 。
。
(2) 。
。
 。
。(2)
 。
。(1)由受力平衡可得: ,
, ,小球带正电荷。
,小球带正电荷。
(2)解法(一)由动能定理可知: ,
, ,又因为
,又因为 ,则
,则 所以
所以 ,得:
,得: 。
。
解法(二)利用等效场(重力和电场力所构成的复合场)当细线离开竖直的位置偏角为α时,小球处于平衡的位置为复合场的平衡位置,即“最低”位置,小球的振动关于该平衡位置对称,可知 。
。
 ,
, ,小球带正电荷。
,小球带正电荷。(2)解法(一)由动能定理可知:
 ,
, ,又因为
,又因为 ,则
,则 所以
所以 ,得:
,得: 。
。解法(二)利用等效场(重力和电场力所构成的复合场)当细线离开竖直的位置偏角为α时,小球处于平衡的位置为复合场的平衡位置,即“最低”位置,小球的振动关于该平衡位置对称,可知
 。
。
练习册系列答案
相关题目

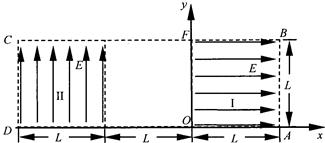 小题1:在该区域AB边的中点处由静止释放电子, 求电子离开ABCD区域的位置。
小题1:在该区域AB边的中点处由静止释放电子, 求电子离开ABCD区域的位置。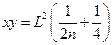

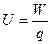 ,说明两点间的电势差U与电场力做功W成正比,与移动电荷的电量q成反比。
,说明两点间的电势差U与电场力做功W成正比,与移动电荷的电量q成反比。

