��Ŀ����
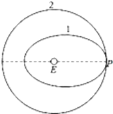
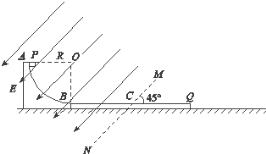
����Ŀ����ͼ��ʾ���ڽ���MN���Ϸ��ռ����б�����·���ˮƽ����н�Ϊ45������ǿ�ų�����ǿ��С![]() ��һ�뾶ΪR=0.8m��
��һ�뾶ΪR=0.8m��![]() �⻬��ԵԲ�����۹̶���ˮƽ���ϣ�һ������Ϊ�ʵ������m=0.2kg���������Сq=1��10��5C�Ĵ����������P�Ӳ۶���A�ɾ�ֹ�ͷţ��Ӳ۵�B������۵�ƽ��ľ�Ե��ľ��Q����ľ��Q�㹻�������ڹ⻬ˮƽ���ϣ�����ΪM=1kg����֪��ʼʱ��ľ����һ�������ڵ糡�У�ͼ��CΪ����MN�볤ľ��Q�Ľ��㣬B��C��ľ���XBC=0.6m�����P��ľ��Q֮��Ķ�Ħ������Ϊ��=
�⻬��ԵԲ�����۹̶���ˮƽ���ϣ�һ������Ϊ�ʵ������m=0.2kg���������Сq=1��10��5C�Ĵ����������P�Ӳ۶���A�ɾ�ֹ�ͷţ��Ӳ۵�B������۵�ƽ��ľ�Ե��ľ��Q����ľ��Q�㹻�������ڹ⻬ˮƽ���ϣ�����ΪM=1kg����֪��ʼʱ��ľ����һ�������ڵ糡�У�ͼ��CΪ����MN�볤ľ��Q�Ľ��㣬B��C��ľ���XBC=0.6m�����P��ľ��Q֮��Ķ�Ħ������Ϊ��=![]() ��ȡ
��ȡ![]() ��
��
(1)������P��A�㻬��B��ʱ���ٶȵĴ�С��
(2)������P��B�㻬��ľ��Q���뿪�糡������������ʱ�䣻
(3)������P�ӻ���Q���뿪�糡�Ĺ�����Ħ��������������
���𰸡�(1) 4m/s�� (2) 0.2s�� (3) 0.85J
��������
![]() �������A��B���̣��糡������Ϊ�㣬�����ܲ��䣬�������غ㶨�ɵ�
�������A��B���̣��糡������Ϊ�㣬�����ܲ��䣬�������غ㶨�ɵ�
![]() ��
��
�������ݽ��vB=4m/s��
![]() ��B�㻬��ľ��Q���뿪�糡���̣����������ȼ����˶�������ٶ�Ϊ
��B�㻬��ľ��Q���뿪�糡���̣����������ȼ����˶�������ٶ�Ϊ![]() ����ţ�ٵڶ����ɵã�
����ţ�ٵڶ����ɵã�
![]() ��
��
���ٶ�λ�ƹ�ʽ�ã�
![]() ��
��
�������ݽ��![]() ��
��![]()
��B�㻬��ľ��Q���뿪�糡������������ʱ�䣺
![]() ��
��
![]() ��������P�ڵ糡���˶�ʱ����ľ��ļ��ٶȴ�С
��������P�ڵ糡���˶�ʱ����ľ��ļ��ٶȴ�С![]() ����ţ�ٵڶ����ɿɵ�
����ţ�ٵڶ����ɿɵ�
![]()
������ֵ�����![]() ��
��
�������P���뿪�糡ʱ��Q����ٶ�Ϊ
![]() ��
��
���P�뿪�糡��ϵͳ�����غ㣬Q���㹻������P��Q���չ���Ϊv��ȡ����Ϊ�������ɶ����غ㶨����
![]() ��
��
���v=0.5 m/s��
������ת�����غ㶨�ɣ�ȫ����Ħ����������
![]() ��
��
�糡��ֻ��BC�ζԽ�����P������
![]() ��
��
���Q=0.85J��
�𣺣�1��������P��A�㻬��B��ʱ���ٶȵĴ�СΪ4m/s��
��2��������P��B�㻬��ľ��Q���뿪�糡������������ʱ��Ϊ0.2s��
��3��������P�ӻ���Q���뿪�糡�Ĺ�����Ħ������������Ϊ0.85J��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�