ЬтФПФкШн
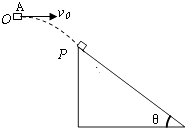
ЁОЬтФПЁПЃЈ20ЗжЃЉФГаЫШЄаЁзщЩшМЦСЫвЛжжЪЕбщзАжУЃЌгУРДбаОПХізВЮЪЬтЃЌЦфФЃаЭШчЬтЭМЫљЪОВЛгУЭъШЋЯрЭЌЕФЧсЩўНЋNИіДѓаЁЯрЭЌЁЂжЪСПВЛЕШЕФаЁЧђВЂСааќЙвгквЛЫЎЦНИЫЁЂЧђМфгаЮЂаЁМфИєЃЌДгзѓЕНгвЃЌЧђЕФБрКХвРДЮЮЊ1ЁЂ2ЁЂ3ЁЁNЃЌЧђЕФжЪСПвРДЮЕнМѕЃЌУПЧђжЪСПгыЦфЯрСкзѓЧђжЪСПжЎБШЮЊkЃЈkЃМ1![]() .НЋ1КХЧђЯђзѓРЦ№ЃЌШЛКѓгЩОВжЙЪЭЗХЃЌЪЙЦфгы2КХЧђХізВЃЌ2КХЧђдйгы3КХЧђХізВЁЁЫљгаХізВНдЮЊЮоЛњаЕФмЫ№ЪЇЕФе§Хі.ЃЈВЛМЦПеЦјзшСІЃЌКіТдЩўЕФЩьГЄЃЌgШЁ10 m/s2ЃЉ
.НЋ1КХЧђЯђзѓРЦ№ЃЌШЛКѓгЩОВжЙЪЭЗХЃЌЪЙЦфгы2КХЧђХізВЃЌ2КХЧђдйгы3КХЧђХізВЁЁЫљгаХізВНдЮЊЮоЛњаЕФмЫ№ЪЇЕФе§Хі.ЃЈВЛМЦПеЦјзшСІЃЌКіТдЩўЕФЩьГЄЃЌgШЁ10 m/s2ЃЉ
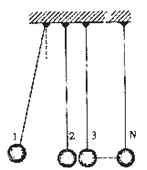
ЃЈ1ЃЉЩшгыn+1КХЧђХізВЧАЃЌnКХЧђЕФЫйЖШЮЊvn,Чѓn+1КХЧђХізВКѓЕФЫйЖШ.
ЃЈ2ЃЉШєNЃН5,дк1КХЧђЯђзѓРИпhЕФЧщПіЯТЃЌвЊЪЙ5КХЧђХізВКѓЩ§Ип16kЃЈ16 hаЁгкЩўГЄЃЉЮЪkжЕЮЊЖрЩйЃП
ЃЈ3ЃЉдкЕкЃЈ2ЃЉЮЪЕФЬѕМўЯТЃЌаќЙвФФИіЧђЕФЩўзюШнвзЖЯЃЌЮЊЪВУДЃП
ЁОД№АИЁПЃЈ1ЃЉvn-1=![]()
ЃЈ2ЃЉk=![]()
ЃЈ3ЃЉаќЙв1КХЧђЕФЩўзюШнвзЖЯ.
ЁОНтЮіЁПЃЈ1ЃЉЩшnКХЧђжЪСПЮЊm,n+1ЃЌХізВКѓЕФЫйЖШЗжБ№ЮЊ![]() ШЁЫЎЦНЯђгвЮЊе§ЗНЯђЃЌОнЬтвтгаnКХЧђгыn+1КХЧђХізВЧАЕФЫйЖШЗжБ№ЮЊvnЁЂ0ЁЂmn+1
ШЁЫЎЦНЯђгвЮЊе§ЗНЯђЃЌОнЬтвтгаnКХЧђгыn+1КХЧђХізВЧАЕФЫйЖШЗжБ№ЮЊvnЁЂ0ЁЂmn+1![]()
ИљОнЖЏСПЪиКуЃЌга![]() ЃЈ1ЃЉ
ЃЈ1ЃЉ
ИљОнЛњаЕФмЪиКуЃЌга![]() =
=![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ
гЩЃЈ1ЃЉЁЂЃЈ2ЃЉЕУ![]()
Щшn+1КХЧђгыn+2КХЧђХіЧАЕФЫйЖШЮЊEn+1
ОнЬтвтгаvn-1=![]()
ЕУvn-1=![]() =
=![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ
ЃЈ2ЃЉЩш1КХЧђАкжСзюЕЭЕуЪБЕФЫйЖШЮЊv1,гЩЛњаЕФмЪиКуЖЈТЩга
![]() ЃЈ4ЃЉ
ЃЈ4ЃЉ
v1=![]() ЃЈ5ЃЉ
ЃЈ5ЃЉ
ЭЌРэПЩЧѓЃЌ5КХЧђХіКѓЫВМфЕФЫйЖШ
![]() ЃЈ6ЃЉ
ЃЈ6ЃЉ
гЩЃЈ3ЃЉЪНЕУ![]() ЃЈ7ЃЉ
ЃЈ7ЃЉ
N=n=5ЪБЃЌv5=![]() ЃЈ8ЃЉ
ЃЈ8ЃЉ
гЩЃЈ5ЃЉЁЂЃЈ6ЃЉЁЂЃЈ8ЃЉШ§ЪНЕУ
k=![]()
![]() ЃЈ9ЃЉ
ЃЈ9ЃЉ
ЃЈ3ЃЉЩшЩўГЄЮЊl,УПИіЧђдкзюЕЭЕуЪБЃЌЯИЩўЖдЧђЕФРСІЮЊF,гЩХЃЖйЕкЖўЖЈТЩга
![]() ЃЈ10
ЃЈ10
дђ![]() ЃЈ11ЃЉ
ЃЈ11ЃЉ
ЃЈ11ЃЉЪНжаEknЮЊnКХЧђдкзюЕЭЕуЕФЖЏФм
гЩЬтвт1КХЧђЕФжиСІзюДѓЃЌгжгЩЛњаЕФмЪиКуПЩжЊ1КХЧђдкзюЕЭЕуХіЧАЕФЖЏФмвВзюДѓЃЌИљОнЃЈ11ЃЉЪНПЩХаЖЯдк1КХЧђХіЧАЫВМфаќЙв1КХЧђЯИЩўЕФеХСІзюДѓЃЌЙЪаќЙв1КХЧђЕФЩўзюШнвзЖЯ.