��Ŀ����
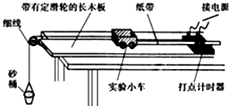
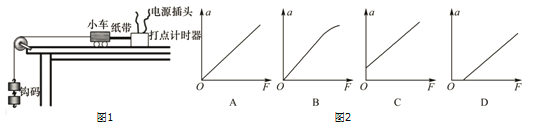
����Ŀ����ͼ����ʾ����Ϊ4 m��ˮƽ���AB��뾶ΪR��0.6 m����ֱ��Բ�����BC��B�������ӣ���һ����Ϊ1 kg�Ļ���(��С����)����A���ɾ�ֹ��ʼ��ˮƽ���ҵ���F���ã�F�Ĵ�С��λ�Ʊ仯�Ĺ�ϵ��ͼ����ʾ��������AB��Ķ�Ħ������Ϊ����0.3����BC��Ķ�Ħ������δ֪��ȡg��10 m/s2����

(1)���鵽��B��ʱ���ٶȴ�С��
(2)������B��ʱ��ȥ��F�������ذ�Բ������ڲ��ϻ�����ǡ���ܵ�����ߵ�C���� �� ���鵽��C��ʱ���ٶ�vc��С? �� �����ڰ�Բ������Ͽ˷�Ħ���������Ĺ��Ƕ��٣� �� �������ڹ���ϵ�λ����B���ˮƽ����Ϊ����
���𰸡���1��6 m/s ��2��![]() 3 J 1.2m
3 J 1.2m
������������������Ի����A��B�Ĺ��̣��ɶ��ܶ����ɵû��鵽��B��ʱ���ٶȣ�����ţ�ٵڶ��������C����ٶȣ��ٸ��ݶ��ܶ�������˷�Ħ�������Ĺ�����������ƽ���˶���ʽ���ˮƽ���롣
��1���Ի����A��B�Ĺ��̣��ɶ��ܶ�����![]()
�������ݽ����vB��6 m/s
(2)��������ǡ���ܵ�����ߵ�Cʱ�������ṩ�������� ![]()
�������ݽ�ã� ![]()
���Ի����B��C�Ĺ��̣��ɶ��ܶ����ã� ![]()
������ֵ����W����3J�����˷�Ħ�������Ĺ�Ϊ3 J
�������뿪C����ƽ���˶�����ˮƽ���� ![]()
����ֱ���� ![]()
������ã�x=1.2m

 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�