题目内容
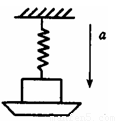
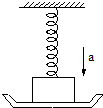如图所示，在劲度系数为k的弹簧下端挂有质量为m的物体，开始用托盘托住物体，使弹簧保持原长，然后托盘以加速度a匀加速下降（a＜g），求经过多长时间托盘与物体分离．
解：当托盘以a匀加速下降时，托盘与物体具有相同的加速度，在下降过程中，物体所受的弹力逐渐增大，支持力逐渐减小，当托盘与物体分离时，支持力为零．设弹簧的伸长量为x，以物体为研究对象，根据牛顿第二定律有：
mg-kx=ma
所以：x=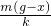
再由运动学公式，有：x=
at2
故托盘与物体分离所经历的时间为：t=
答：经过托盘与物体分离．
分析：随着托盘的下降，弹簧的伸长量逐渐变大，所以物体受到的弹簧向上的拉力逐渐增大，托盘的支持力逐渐减小，当支持力恰好为零时，二者即将分离，此时物体的加速度与托盘的加速度仍然相等，由此可计算出弹簧的伸长量即托盘下降的距离，从而利用匀变速运动的公式得到时间
点评：找到托盘与物体分力的临界点时：两者之间的作用力为零；找到另一个等量关系：弹簧的伸长量就是托盘的下降距离
mg-kx=ma
所以：x=
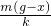
再由运动学公式，有：x=
at2故托盘与物体分离所经历的时间为：t=
答：经过
托盘与物体分离．分析：随着托盘的下降，弹簧的伸长量逐渐变大，所以物体受到的弹簧向上的拉力逐渐增大，托盘的支持力逐渐减小，当支持力恰好为零时，二者即将分离，此时物体的加速度与托盘的加速度仍然相等，由此可计算出弹簧的伸长量即托盘下降的距离，从而利用匀变速运动的公式得到时间
点评：找到托盘与物体分力的临界点时：两者之间的作用力为零；找到另一个等量关系：弹簧的伸长量就是托盘的下降距离
练习册系列答案
相关题目
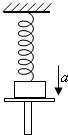（2007?孝感一模）如图所示，在劲度系数为k的弹簧下端挂一质量为m的物体，物体下有一托盘，用托盘托着物体使弹簧恰好处于原长．然后使托盘以加速度a竖直向下做匀加速直线运动（a＜g），试求托盘向下运动多长时间能与物体脱离？
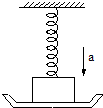如图所示，在劲度系数为k的弹簧下端挂有质量为m的物体，开始用托盘托住物体，使弹簧保持原长，然后托盘以加速度a匀加速下降（a＜g），求经过多长时间托盘与物体分离．
如图所示，在劲度系数为k的弹簧下端挂一质量为m的物体，物体下有一托盘，用托盘托着物体使弹簧恰好处于原长，然后使托盘以加速度a竖直向下做匀加速直线运动（a＜g）试求：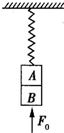
如图所示，在劲度系数为k=100N/m的轻弹簧下端拴一质量为mA=1kg的小物体A，紧挨着A有一物体B，B的质量为mB=2kg，开始时对B施加一个大小为F0=38N的竖直向上的力，系统处于静止状态．撤去F0，同时对B施加一竖直向上的作用力F使物体B以加速度a=2m/s2匀加速下降，g=10m/s2，求经过多长时间A、B分离？