题目内容
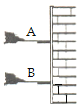
【题目】如图所示,MN、PQ是两条水平、平行放置的光滑金属导轨,导轨的一端接理想变压器的原线圈,变压器的副线圈与电阻R=20 Ω组成闭合回路,变压器的原副线圈匝数之比n1∶n2=1∶10,导轨宽L=5 m.质量m=2 kg、电阻不计的导体棒ab垂直MN、PQ放在导轨上,在水平外力F作用下,从t=0时刻开始在图示的两虚线范围内往复运动,其速度随时间变化的规律是v=2sin20πt(m/s).垂直轨道平面的匀强磁场的磁感应强度B=4 T.导轨、导线和线圈电阻均不计.求:

(1)ab棒中产生的电动势的表达式;ab棒中产生的是什么电流?
(2)电阻R上的电热功率P.
(3)从t=0到t1=0.025 s的时间内,外力F所做的功.
【答案】(1)E=BLv=40sin20πt(V);正弦交变电流(2)4×103W(3)104J
【解析】(1)ab棒中产生的电动势的表达式为![]()
故ab棒中产生的是正弦交变电流.
(2)设原线圈上电压的有效值为U1,则![]()
设副线圈上电压的有效值为![]() ,则
,则![]() ,解得
,解得![]()
电阻R上的电热功率![]()
(3)由以上分析可知,该正弦交流电的周期![]() .
.
从t=0到t1=0.025s,经历了四分之一个周期.设在这段时间内电阻R上产生的热量为Q,则![]()
在t1=0.025s时刻,ab棒的速度为v,则![]()
由能量守恒定律可得这段时间内外力F做的功![]()

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目