题目内容
2.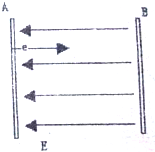 如图,真空中的A、B两正负电极板间有一匀强电场,两极板间电势差为U,场强为E,极板A点上的一个带电量为q、质量为m的电荷由静止出发,运动到相距d的极板B上,求:
如图,真空中的A、B两正负电极板间有一匀强电场,两极板间电势差为U,场强为E,极板A点上的一个带电量为q、质量为m的电荷由静止出发,运动到相距d的极板B上,求:(1)电荷运动的加速度是多少?
(2)电荷到达正极板时的速度多大?
分析 (1)由匀强电场的电势差与电场强度的关系求出E,在得到F,由牛顿第二定律得到加速度;
(2)由动能定理求得速度
解答 解:(1)由牛顿第二定律可得:a=$\frac{F}{m}=\frac{Eq}{m}$…①
而E=$\frac{U}{d}$…②
由①②得:a=$\frac{Uq}{dm}$
(2)由动能定理可得:Uq=$\frac{1}{2}$mv2
故v=$\sqrt{\frac{2Uq}{m}}$
答:(1)电荷运动的加速度是$\frac{Uq}{dm}$
(2)电荷到达正极板时的速度为$\sqrt{\frac{2Uq}{m}}$
点评 关键知道匀强电场的电势差与电场强度的关系,由动能定理求速度是比较快的方法,本题虽然简单,但所涉及的知识不少.

练习册系列答案
相关题目
3.一物体放在光滑水平面上,受到三个大小分别为2N、5N和9N的水平拉力作用,则该物体所受的合力可能为 ( )
| A. | 0 | B. | 10N | C. | 20N | D. | 30N |
7. 如图所示,带有正电荷的A粒子和B粒子同时从匀强磁场的边界上的P点分别以30°和60°(与边界的交角)射入磁场,又同时从磁场边界上的Q点飞出,设边界上方的磁场范围足够大,则下列说法中正确的是( )
如图所示,带有正电荷的A粒子和B粒子同时从匀强磁场的边界上的P点分别以30°和60°(与边界的交角)射入磁场,又同时从磁场边界上的Q点飞出,设边界上方的磁场范围足够大,则下列说法中正确的是( )
 如图所示,带有正电荷的A粒子和B粒子同时从匀强磁场的边界上的P点分别以30°和60°(与边界的交角)射入磁场,又同时从磁场边界上的Q点飞出,设边界上方的磁场范围足够大,则下列说法中正确的是( )
如图所示,带有正电荷的A粒子和B粒子同时从匀强磁场的边界上的P点分别以30°和60°(与边界的交角)射入磁场,又同时从磁场边界上的Q点飞出,设边界上方的磁场范围足够大,则下列说法中正确的是( )| A. | A粒子运动的速率可能跟B粒子的相等 | |
| B. | A粒子做完圆周运动的周期比B粒子的小 | |
| C. | A粒子的轨迹半径比B粒子的轨迹半径大 | |
| D. | 若A粒子是α粒子,则B粒子可能是质子 |
11.两个力F1和F2间的夹角为θ,两力的合力为F,以下说法正确的是( )
| A. | 合力F总比分力F1和F2中任何一个力都大 | |
| B. | 若F1和F2大小不变,θ越小,合力F就越小 | |
| C. | 如果夹角不变,F1大小不变,只要F2增大,合力F不一定变大 | |
| D. | 物体同时受到F1、F2与F的作用 |
12.如图所示,倾角为α的足够大的光滑斜面上,有一个xOy直角坐标系,x轴沿水平方向.若将光滑金属小球从O点分别施以不同的初始运动条件,关于其后的运动规律,下列分析不正确的有( )


| A. | 将小球以初速度v0分别沿x轴正方向和y轴负方向抛出,到达斜面底边时速度大小相等 | |
| B. | 将小球以速度v0沿x轴正方向抛出和由静止释放,到达斜面底边的时间相同 | |
| C. | 将小球以初速度v0分别沿x轴正方向和y轴负方向抛出,将同时到达斜面底边 | |
| D. | 无论怎样将小球沿斜面抛出或由静止释放,小球做的都是匀变速运动,加速度大小均为gsinα |
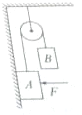 如图所示,物体A重50N,A与墙面动摩擦因数μ=0.3,现用F=100N的力压着物体A,此时物体A既不上滑,也不下滑,求物体B的重力范围.(设最大静摩擦力等于滑动摩擦力)
如图所示,物体A重50N,A与墙面动摩擦因数μ=0.3,现用F=100N的力压着物体A,此时物体A既不上滑,也不下滑,求物体B的重力范围.(设最大静摩擦力等于滑动摩擦力) 如图所示,P是一个放射源,从开口处在纸面内向各个方向放出某种粒子(不计重力),而这些粒子最终必须全部垂直射到底片MN这一有效区域,并要求底片MN上每一地方都有粒子到达.假若放射源所放出的是质量为m、电量为q的带正电的粒子,且所有的粒子速率都是v,M与放射源的出口在同一水平面,底片MN竖直放置,底片MN长为L.为了实现上述目的,我们必须在P的出口处放置一有界匀强磁场.则匀强磁场的方向为垂直于纸面向外,匀强磁场的磁感应强度B的大小为$\frac{2mv}{qL}$,最小有界匀强磁场的面积S为$\frac{1}{4}$πL2.
如图所示,P是一个放射源,从开口处在纸面内向各个方向放出某种粒子(不计重力),而这些粒子最终必须全部垂直射到底片MN这一有效区域,并要求底片MN上每一地方都有粒子到达.假若放射源所放出的是质量为m、电量为q的带正电的粒子,且所有的粒子速率都是v,M与放射源的出口在同一水平面,底片MN竖直放置,底片MN长为L.为了实现上述目的,我们必须在P的出口处放置一有界匀强磁场.则匀强磁场的方向为垂直于纸面向外,匀强磁场的磁感应强度B的大小为$\frac{2mv}{qL}$,最小有界匀强磁场的面积S为$\frac{1}{4}$πL2.