题目内容
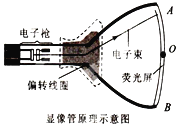
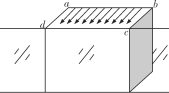
【题目】如图所示，一个边长为L＝0.8 m(ab＝bc＝L)，高为h＝0.8 m的光滑实心立方体固定在水平面上(其中靠外面的cd边所在竖直面足够长，称为“A面”)，上表面处有垂直cd边的匀强电场，方向如图，电场强度为E＝4 N/C，在立方体前方外有竖直向上的匀强磁场。今在a点以不同的速度v0沿ab边射入质量为m、电荷量为q＝
的带正电的小球。试求：(本题可能用到的数据：g＝10 m/s2，π＝3.14，tan α分别等于2、3、4、5时，对应的α的弧度值分别为1.11、1.25、1.33、1.37。如果有碰撞皆为弹性碰撞，但与地面的碰撞是完全非弹性的，最终结果保留两位小数)
(1)如果射入的小球都能从cd边射出，求出速度v0的范围？
(2)满足条件(1)时，如果小球都能直接落在A面之前的水平面上，那么磁感应强度B应满足什么条件？
(3)如果某个小球恰好从dc边中点射出电场，落地点恰好在dc边的正下方的边线上，那么磁感应强度B多大？落地点与射出点的水平距离多大？
【答案】（1）
（2）3.14T（3）3.62n(T);0.88m
【解析】
（1）根据平抛运动的规律求解速度v0的范围；（2）根据圆周运动以及自由落体运动的规律求解磁感应强度B应满足的条件；（3）根据圆周运动的规律，结合几何关系求解磁感应强度B以及落地点与射出点的水平距离.
(1)L＝v0mt，L＝
gt2
所以最大速度为则：v0m＝
，0≤v0≤
0≤v0≤2.00 m/s
(2)如果直接从d点飞出对应的圆心角最小α＝π，做圆运动的最短时间为tmin＝
那么在tmin时间内小球必须着地，自由落体的时间t＝
又t≤tmin，则B≤
＝3.14 T
(3)tan α＝
＝4＝
(α＝1.33)，v0＝
下落过程中，可能与A面发生碰撞，碰撞后不影响竖直方向的运动，但对水平面的运动有影响，如图是水平面内的运动情况图。从M点射出，运动了圆心角为2π－2α角后在N点相碰，然后又运动了圆心角为2π－2α角后再次与A面相碰，因此可能运动了n个这样的圆弧恰好落地，因此小球在磁场中运动的时间为：
t＝
其中n＝1，2，3……
竖直下落的时间为t′＝
所以t＝t′，则有：
则：B＝
＝3.62n(T)(n＝1，2，3……)
射出的速度为v，半径为R＝
，圆心角为2π－2α，所以MN＝2Rsin α
MN＝
，vsin α＝vy＝gt″＝g
＝
所以
距射出点的水平距离为x＝MN·n＝
m＝0.88 m
