题目内容
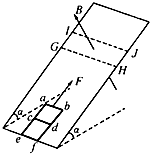 如图所示,一质量m=0.5kg的“日”字形匀质导线框“abdfeca”静止在倾角a=37°的 粗糙斜面上,线框各段长ab=cd=ef=ac=bd=ce=df=L=0.5m,ef与斜面底边重合,线框与斜面间的动摩擦因数μ=0.25,ab、cd、ef三段的阻值相等、均为R═0.4Ω,其余部 分电阻不计.斜面所在空间存在一有界矩形匀强磁场区域GIJH,其宽度GI=HJ=L,长度IJ>L,IJ∥ef,磁场垂直斜面向上,磁感应强度B=1T.现用一大小F=5N、方向沿斜 面向上且垂直于ab的恒力作用在ab中点,使线框沿斜面向上运动,ab进入磁场时线框恰 好做匀速运动.若不计导线粗细,重力加速度g=10m/s2,sin37=0.6,cos37=0.8.求:
如图所示,一质量m=0.5kg的“日”字形匀质导线框“abdfeca”静止在倾角a=37°的 粗糙斜面上,线框各段长ab=cd=ef=ac=bd=ce=df=L=0.5m,ef与斜面底边重合,线框与斜面间的动摩擦因数μ=0.25,ab、cd、ef三段的阻值相等、均为R═0.4Ω,其余部 分电阻不计.斜面所在空间存在一有界矩形匀强磁场区域GIJH,其宽度GI=HJ=L,长度IJ>L,IJ∥ef,磁场垂直斜面向上,磁感应强度B=1T.现用一大小F=5N、方向沿斜 面向上且垂直于ab的恒力作用在ab中点,使线框沿斜面向上运动,ab进入磁场时线框恰 好做匀速运动.若不计导线粗细,重力加速度g=10m/s2,sin37=0.6,cos37=0.8.求:(1)ab进入磁场前线框运动的加速度大小a.
(2)cd在磁场中运动时,外力克服安培力做功的功率P.
(3)线框从开始运动到ef恰好穿出磁场的过程中,线框中产生的焦耳热与外力F做功的比值
| Q | W |
分析:(1)对于线框进入磁场前的运动过程,根据牛顿第二定律求解加速度a的大小.
(2)ab进入磁场时线框恰好做匀速运动,只有一边切割磁感线,当cd在磁场中运动时,有且仅有一条边切割磁感线,等效电路也相同,所以线框一直做匀速运动,根据平衡条件和安培力与速度的关系式,求出线框匀速运动的速度v,即由公式P=F安v求解外力克服安培力做功的功率P.
(3)由运动学公式求出ab进入磁场前线框发生的位移x,外力F做功为W=F(x+3L),线框中产生的焦耳热等于克服安培力所做的功.
(2)ab进入磁场时线框恰好做匀速运动,只有一边切割磁感线,当cd在磁场中运动时,有且仅有一条边切割磁感线,等效电路也相同,所以线框一直做匀速运动,根据平衡条件和安培力与速度的关系式,求出线框匀速运动的速度v,即由公式P=F安v求解外力克服安培力做功的功率P.
(3)由运动学公式求出ab进入磁场前线框发生的位移x,外力F做功为W=F(x+3L),线框中产生的焦耳热等于克服安培力所做的功.
解答:解:(1)ab进入磁场前,线框做匀加速运动,所受的摩擦力大小为:f=μmgcosα=0.25×0.5×10×cos37°N=1N,
由牛顿第二定律有:F-mgsinα-f=ma
代入数据解得:a=
=
m/s2=2m/s2,
(2)由于线框穿越磁场的过程中有且仅有一条边切割磁感线,等效电路也相同,所以线框一直做匀速运动,设速度大小为v,
由力的平衡条件有:
F=mgsinα+μmgcosα+F安
代入数据解得:F安=1N
而安培力F安=BIL=
回路的总电阻为 R总=R+
=0.4+0.2=0.6Ω
解得:v=2.4m/s
所以 P=F安v=2.4W
(3)设ab进入磁场前线框发生的位移为x,
则 x=
=
m=1.44m
而 Q=F安×3L=1×3×0.5J=1.5J
W=F(x+3L)=5×(1.44+3×0.5)J=14.7J
=
=
答:(1)ab进入磁场前线框运动的加速度大小a为2m/s2.
(2)cd在磁场中运动时,外力克服安培力做功的功率P为2.4W.
(3)线框从开始运动到ef恰好穿出磁场的过程中,线框中产生的焦耳热与外力F做功的比值
为
.
由牛顿第二定律有:F-mgsinα-f=ma
代入数据解得:a=
| F-mgsinα-f |
| m |
| 5-0.5×10×sin37°-1 |
| 0.5 |
(2)由于线框穿越磁场的过程中有且仅有一条边切割磁感线,等效电路也相同,所以线框一直做匀速运动,设速度大小为v,
由力的平衡条件有:
F=mgsinα+μmgcosα+F安
代入数据解得:F安=1N
而安培力F安=BIL=
| B2L2v |
| R总 |
回路的总电阻为 R总=R+
| R |
| 2 |
解得:v=2.4m/s
所以 P=F安v=2.4W
(3)设ab进入磁场前线框发生的位移为x,
则 x=
| v2 |
| 2a |
| 2.42 |
| 2×2 |
而 Q=F安×3L=1×3×0.5J=1.5J
W=F(x+3L)=5×(1.44+3×0.5)J=14.7J
| Q |
| W |
| 1.5 |
| 14.7 |
| 5 |
| 49 |
答:(1)ab进入磁场前线框运动的加速度大小a为2m/s2.
(2)cd在磁场中运动时,外力克服安培力做功的功率P为2.4W.
(3)线框从开始运动到ef恰好穿出磁场的过程中,线框中产生的焦耳热与外力F做功的比值
| Q |
| W |
| 5 |
| 49 |
点评:按顺序分析线框的受力情况,确定其运动情况是解决本题的关键点,同时要熟练推导出安培力与速度的关系,知道克服安培力做功等于线框产生的热量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,一质量M=50kg、长L=3m的平板车静止在光滑的水平地面上,平板车上表面距地面的高度h=1.8m.一质量m=10kg可视为质点的滑块,以v0=7.5m/s的初速度从左端滑上平板车,滑块与平板车间的动摩擦因数μ=0.5,取g=10m/s2.
如图所示,一质量M=50kg、长L=3m的平板车静止在光滑的水平地面上,平板车上表面距地面的高度h=1.8m.一质量m=10kg可视为质点的滑块,以v0=7.5m/s的初速度从左端滑上平板车,滑块与平板车间的动摩擦因数μ=0.5,取g=10m/s2. 如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一质量m=1.0kg的小木块A,现以地面为参照系,给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,最后A相对B静止,此时A的速度为( )
如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一质量m=1.0kg的小木块A,现以地面为参照系,给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,最后A相对B静止,此时A的速度为( ) 如图所示,一质量M=2kg的斜面体静止在水平地面上,斜面体与地面间的动摩擦因数为μ=0.5,斜面夹角α=37°.一质量m=1kg的光滑小球放在斜面体与竖直墙壁之间,处于静止状态.若在光滑小球的正上方施加一个竖直向下的力,要使斜面体向右移动,竖直向下的力F至少为多大?(设滑动摩擦力等于最大静摩擦力,g取10m/s2)
如图所示,一质量M=2kg的斜面体静止在水平地面上,斜面体与地面间的动摩擦因数为μ=0.5,斜面夹角α=37°.一质量m=1kg的光滑小球放在斜面体与竖直墙壁之间,处于静止状态.若在光滑小球的正上方施加一个竖直向下的力,要使斜面体向右移动,竖直向下的力F至少为多大?(设滑动摩擦力等于最大静摩擦力,g取10m/s2) (2011?太原模拟)如图所示,一质量m=65kg的选手参加“挑战极限运动”,要在越过宽度s=3m的水沟后跃上高h=1.8m的平台.他采用的方法是:手握长L=3.05m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直(不弯曲),人的重心恰好位于杆的顶端,此刻人放开杆水平飞出,最终落到平台上(重心恰在平台表面).不计运动过程中的空气阻力,取g=10m/s2:
(2011?太原模拟)如图所示,一质量m=65kg的选手参加“挑战极限运动”,要在越过宽度s=3m的水沟后跃上高h=1.8m的平台.他采用的方法是:手握长L=3.05m的轻质弹性杆一端,从A点由静止开始匀加速助跑,至B点时,杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直(不弯曲),人的重心恰好位于杆的顶端,此刻人放开杆水平飞出,最终落到平台上(重心恰在平台表面).不计运动过程中的空气阻力,取g=10m/s2: