题目内容
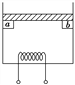
【题目】一开口向上且导热性能良好的气缸如图所示固定在水平面上，用质量和厚度均可忽略不计的活塞封闭一定质量的理想气体，系统平衡时，活塞到气缸底部的距离为h1＝10 cm；外界环境温度保持不变，将质量为2m和m的砝码甲、乙放在活塞上，系统再次平衡时活塞到气缸底部的距离为h2＝5 cm；现将气缸内气体的温度缓缓地升高Δt＝60 ℃，系统再次平衡时活塞到气缸底部的距离为h3＝6 cm；然后拿走砝码甲，使气缸内气体的温度再次缓缓地升高Δt′＝60 ℃，系统平衡时活塞到气缸底部的距离为h4，忽略活塞与气缸之间的摩擦力，求：
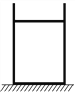
①最初气缸内封闭的理想气体的温度t1为多少摄氏度；
②最终活塞到气缸底部的距离h4为多少．
【答案】①27 ℃ ②10.5 cm
【解析】（1）假设气缸的横截面积为S，气体初态：V1=h1S；P1=P0；温度T1
将甲乙两砝码放在活塞上后，体积V2=h2S；温度T1 ;P2=P0+
；
由玻意耳定律P1 V1= P2 V2
解得P2=2P1=2P0，
即
气缸内气体的温度升高60℃时，温度为T3=T1+60；体积为V3=h3S，
经等压变化，则由盖吕萨克定律
解得T1=300K 即t1=T1-273=27℃
（2）如果拿走砝码甲，使气缸内气体的温度再次缓慢升高
时，压强P4=P0+
=
,体积V4=h4S；温度
由理想气体状态变化方程
解得：h4=10.5cm
练习册系列答案
长江作业本同步练习册系列答案
相关题目
