题目内容
【题目】回旋加速器在科学研究中得到了广泛应用,其原理如图所示。D1和D2是两个中空的半圆形金属盒,置于与盒面垂直的匀强磁场中,它们接在电压为U、周期为T的交流电源上。位于D1圆心处的质子源A能不断产生质子(初速度可以忽略),它们在两盒之间被电场加速。当质子被加速到最大动能Ek后,再将它们引出。忽略质子在电场中的运动时间,则下列说法中正确的是( )
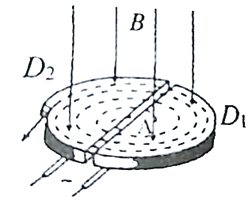
A. 若只增大交变电压U,则质子的最大动能Ek会变大
B. 若只增大交变电压U,则质子在回旋加速器中运行的时间不变。
C. 若只将交变电压的周期变为2T,仍能用此装置持续加速质子
D. 质子第n次被加速前、后的轨道半径之比为![]()
【答案】D
【解析】
回旋加速器是通过电场进行加速,磁场进行偏转来加速带电粒子.带电粒子在磁场中运动的周期与交流电源的周期相同,根据![]() 比较周期.当粒子最后离开回旋加速器时的速度最大,根据
比较周期.当粒子最后离开回旋加速器时的速度最大,根据![]() 求出粒子的最大速度,从而得出最大动能的大小关系。
求出粒子的最大速度,从而得出最大动能的大小关系。
A项:根据![]() 得
得![]() ,则最大动能
,则最大动能![]() ,与加速电压无关,故A错误;
,与加速电压无关,故A错误;
B项:若只增大交变电压U,则质子在回旋加速器中加速次数会减小,导致运行时间变短,故B错误;
C项:若只将交变电压的周期变为2T,而质子在磁场中运动的周期不变,则两周期不同,所以不能始终处于加速状态,故C错误;
D项:根据洛伦兹力提供向心力做匀速圆周运动,则有半径公式![]() 与
与![]() ,所以质子第n次被加速前后的轨道半径之比为
,所以质子第n次被加速前后的轨道半径之比为![]() ,故D正确。
,故D正确。
故选:D。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目