��Ŀ����
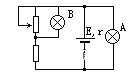
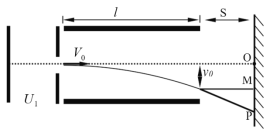
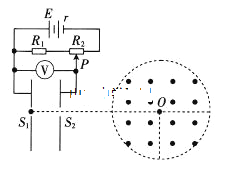
����Ŀ����ͼ��ʾ����Բ��ΪO���뾶R=5cm����ֱԲ�������ڣ���һ������ֱ��Բ�������������ǿ�ų�����ֱƽ�з��õĽ�����������ͼʾ��·�У���Դ�綯��E=220V������r=5![]() ����ֵ�������ֵR1=16
����ֵ�������ֵR1=16![]() ������������R2�������ֵRmax=199
������������R2�������ֵRmax=199![]() �����������ϵ�С��S1��S2��Բ��O�ڴ�ֱ�ڼ����ͬһֱ���ϣ����бȺ�
�����������ϵ�С��S1��S2��Բ��O�ڴ�ֱ�ڼ����ͬһֱ���ϣ����бȺ�![]() �Ĵ�����������С��S1����糡���ٺ�С��S2�����Ȼ��ֱ����ų����Ӵų��������������������ƬP��λ�ò�ͬ�������ڴų����˶���ʱ��Ҳ��ͬ���������ѹ����ʾ��U=100Vʱ�����Ӵ�Բ���������͵���ֱ���´����ų�����������������������С��S1���ij��ٶȣ�ȡtan68.2��=2.5����
�Ĵ�����������С��S1����糡���ٺ�С��S2�����Ȼ��ֱ����ų����Ӵų��������������������ƬP��λ�ò�ͬ�������ڴų����˶���ʱ��Ҳ��ͬ���������ѹ����ʾ��U=100Vʱ�����Ӵ�Բ���������͵���ֱ���´����ų�����������������������С��S1���ij��ٶȣ�ȡtan68.2��=2.5����
(1)U=100Vʱ�����Ӵ�С��S2����ʱ���ٶȴ�Сv0��
(2)��ǿ�ų��ĴŸ�Ӧǿ�ȴ�СB��
(3)�����ڴų����˶����ʱ��t��(���������λ��Ч����)
���𰸡���1��8��103m/s��2��0.5T��3��1.5��10-5s
��������
��1�������ڵ糡�м��٣��ɶ��ܶ��������������ʱ���ٶȴ�С����2�������ڴų�����Բ���˶������ݼ��ι�ϵ����뾶���ٸ���ţ�ٵڶ����ɼ�������Ÿ�Ӧǿ�ȣ���3�����ݱպϵ�·��ŷķ���ɡ����ܶ�����ţ�ٵڶ����ɺͼ��ι�ϵ������������ڴų����˶����ʱ�䡣
��1���������ڵ糡�е��˶������У��ɶ��ܶ����У�![]()
��ã�![]()
��2�����Ӵ�Բ���������͵���ֱ���´����ų����������ڴų��е��ٶȷ���ƫת��![]() �������ڴų�����Բ���˶��ľ�����ͼ����ʾ��
�������ڴų�����Բ���˶��ľ�����ͼ����ʾ��
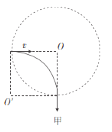
�ɼ��ι�ϵ��֪�������ڴų�����Բ���˶��İ뾶Ϊ��![]()
��ţ�ٵڶ������У�![]()
��ã�![]()
��3�����������ĵ�ѹԽС�����Ӿ��糡���ٺ���ٶ�ԽС�������ڴų�����Բ���˶��İ뾶ԽС������糡ʱ��ƫת��Խ���ڴų����˶���ʱ��Խ�������Ի�Ƭ�ڱ�����![]() �����ʱ�������ڴų����˶���ʱ������ɱպϵ�·��ŷķ�����У�
�����ʱ�������ڴų����˶���ʱ������ɱպϵ�·��ŷķ�����У�![]()
������������С��ѹΪ![]()
�����Ӽ��ٺ���ٶȴ�СΪv���ɶ��ܶ����У�![]()
��������Բ���˶��İ뾶Ϊ![]() ����ţ�ٵڶ������У�
����ţ�ٵڶ������У�![]()
��ã�![]()
���ӽ���ų���ľ�����ͼ����ʾ��
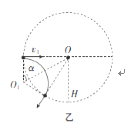
![]() Ϊ����Բ��Բ�ģ��ɼ��ι�ϵ�У�
Ϊ����Բ��Բ�ģ��ɼ��ι�ϵ�У�![]()
��ã�![]()
��![]() ������
������![]()
��ã�![]()