Question

一个重力不计的带电粒子经电场加速后沿平行金属板间的中线射入平行金属板间。已知金属板间电压为U，间距为d，极板间匀强磁场的磁感应强度为B₁，方向垂直纸面向里，若带电粒子在极板间刚好沿中线运动，离开极板后，沿x轴方向射入半径为r，磁感应强度为B₂的圆形磁场区域（圆心为坐标原点），如图所示。最后粒子恰好从圆形磁场边界与y轴的交点C处沿y轴方向飞出。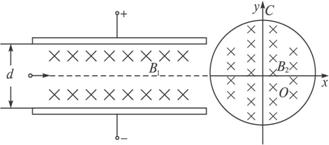

求：（1）该粒子带何种电荷，粒子运动速度v多大？

（2）粒子的比荷为多少？

（3）若将圆形磁场的磁感应强度由B₂变为3B₂，粒子在圆形磁场中运动的时间t为多少？

Answer 1

解：（1）粒子在圆形磁场中向上偏，所以带正电。

粒子在极板间运动，满足qE=qvB₁;

又E=，

则v=。

（2）因粒子离开B₂沿y轴方向，故在B₂中方向改变了90°，即运动了圆周。则R=r₁

因此=r，所以。

（3）若B₂变为3B₂，则R′=,则t=T,

T=,所以t=。