题目内容
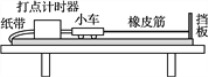
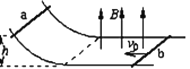
【题目】如图所示,两足够长且不计其电阻的光滑金属轨道,如图所示放置,间距为d=1m,在左端斜轨道部分高h=1.25m处放置一金属杆a,斜轨道与平直轨道区域以光滑圆弧连接,在平直轨道右端放置另一金属杆b,杆a、b电阻Ra=2Ω、Rb=5Ω,在平直轨道区域有竖直向上的匀强磁场,磁感强度B=2T.现杆b以初速度v0=5m/s开始向左滑动,同时由静止释放杆a,杆a由静止滑到水平轨道的过程中,通过杆b的平均电流为0.3A;从a下滑到水平轨道时开始计时, a、b杆运动速度-时间图象如图所示(以a运动方向为正),其中ma=2kg,mb=1kg,g=10m/s2,求:

(1)杆a进入水平轨道的速度va和杆a在斜轨道上运动的时间t;
(2)杆a在水平轨道上运动过程中通过其截面的电量q;
(3)在整个运动过程中杆b产生的焦耳热Qb。
【答案】(1)5s(2)7/3C(3)115/6J
【解析】(1)对杆a下滑的过程中,机械能守恒:mgh=![]() mava2
mava2
![]()
对b棒运用动量定理有: ![]()
其中vb0=2m/s
代入数据得到:Δt=5s
(2)设最后两杆共同的速度为v′,由动量守恒得: ![]()
代入数据计算得出: ![]()
杆a动量变化等于它所受安培力的冲量,由动量定理可得I安=BIdΔt,=mava -mav
而 q=IΔt=7/3C
(3)由能量守恒得,共产生的焦耳热为![]()
解得:Q=![]() J
J
b棒中产生的焦耳热为 ![]()

练习册系列答案
相关题目