题目内容
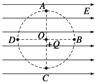
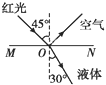
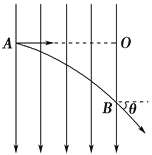
【题目】如图所示,质量为m,电荷量为e的粒子从A点以v0的速度沿垂直电场线方向的直线AO方向射入匀强电场,由B点飞出电场是速度方向与AO方向成45°,已知AO的水平距离为d。(不计重力;)求:
(1)从A点到B点用的时间;
(2)匀强电场的电场强度大小;
(3)AB两点间电势差.
【答案】(1)![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:粒子从A点以v0的速度沿垂直电场线方向射入电场,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,由水平距离d和初速度v0可求出时间;将粒子射出电场的速度进行分解,求出竖直方向分速度vy,由牛顿第二定律和vy=at结合求出电场强度E;由动能定理可求解AB两点间电势差。
(1)粒子从A点以v0的速度沿垂直电场线方向射入电场,
水平方向做匀速直线运动,则有: ![]()
解得: ![]()
(2)由牛顿第二定律得: ![]()
将粒子射出电场的速度v进行分解,则有 vy=v0tan45°=v0
根据速度时间关系:vy=at
联立解得: ![]()
(3)由动能定理得: ![]()
解得: ![]()
试题分析:本题主要考查了运动的分解法研究类平抛运动,关键将速度进行分解,由牛顿第二定律和运动学公式相结合进行解题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目