题目内容
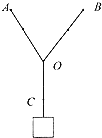
【题目】如图所示,质量![]() 的物体置于可绕竖直轴匀速转动的平台上,m用细绳通过光滑的定滑轮与质量为
的物体置于可绕竖直轴匀速转动的平台上,m用细绳通过光滑的定滑轮与质量为![]() 的物体相连,m悬于空中与M都处于静止状态,假定M与轴O的距离
的物体相连,m悬于空中与M都处于静止状态,假定M与轴O的距离![]() ,与平台的最大静摩擦力为其重力的
,与平台的最大静摩擦力为其重力的![]() 倍,试问:
倍,试问:

![]() 受到的静摩擦力最小时,平台转动的角速度
受到的静摩擦力最小时,平台转动的角速度![]() 为多大?
为多大?
![]() 要保持M与平台相对静止,M的线速度的范围?
要保持M与平台相对静止,M的线速度的范围?
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】(1)物体A与圆盘保持相对静止且不受摩擦力时,绳子的拉力提供向心力,由牛顿第二定律得:
![]()
带入数据得: ![]()
(2)设此平面角速度![]() 的最小值为
的最小值为![]() ,此时M所受的静摩擦力达到最大,方向沿半径向外,则由牛顿第二定律得:
,此时M所受的静摩擦力达到最大,方向沿半径向外,则由牛顿第二定律得:
![]() ,
,
又![]()
联立得: ![]() ,
,
代入数据解得: ![]()
设此平面角速度![]() 的最大值为
的最大值为![]() ,此时M所受的静摩擦力达到最大,方向沿半径向里,则由牛顿第二定律得:
,此时M所受的静摩擦力达到最大,方向沿半径向里,则由牛顿第二定律得:
![]() ,
,
又![]()
代入解得: ![]()
故为使m处于静止状态,角速度![]() 的何值范围为:
的何值范围为: ![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目