��Ŀ����
��ͼ���ǹ̶���ˮƽ���ϵĺ����Ϊ��

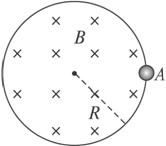
���εĹ⻬��ֱ����ۣ��ۿ����ϣ����ڷ���һ�������飬�������а뾶ΪR�İ�Բ���ι⻬���ۣ���������Ŀ���Ϊ2R���ȡ�

���β۵Ŀ�����С�����а뾶Ϊr��r����R���Ľ���С����ˮƽ���ٶ�v0���飬�ӻ����ϵİ�Բ�βۿڱ�Ե���룮��֪����С�������Ϊm���������������Ϊ3m��ȫ��������е����ʧ����
��1��������С�����������ʱ������С��ͽ���������ٶȸ��Ƕ��
��2��������С�����������ϵİ�Բ���β۵ĵײ�A��ʱ���Խ���������������Ƕ��

���εĹ⻬��ֱ����ۣ��ۿ����ϣ����ڷ���һ�������飬�������а뾶ΪR�İ�Բ���ι⻬���ۣ���������Ŀ���Ϊ2R���ȡ�

���β۵Ŀ�����С�����а뾶Ϊr��r����R���Ľ���С����ˮƽ���ٶ�v0���飬�ӻ����ϵİ�Բ�βۿڱ�Ե���룮��֪����С�������Ϊm���������������Ϊ3m��ȫ��������е����ʧ����
��1��������С�����������ʱ������С��ͽ���������ٶȸ��Ƕ��
��2��������С�����������ϵİ�Բ���β۵ĵײ�A��ʱ���Խ���������������Ƕ��

��1��С���뻬������ù����У���ˮƽ�������غ㣬���У�mv0=mv1+3mv2
����Ϊϵͳ��е���غ㣺
m
=
m
+
3m
�� v1=-
v0����������v2=
v0���������ң�
��2��������С��ͨ��A��ʱ���ص��췽�����С�������������й�ͬ�ٶ�v����A�����߷�����ٶ�Ϊv�䣬�ɶ����غ�ͻ�е���غ��
mv0=��m+3m��v
m
=
(m+3m)v2+
mv��2
��� v��=
v0
��ţ�ٵڶ����ɵ�N=
=
��Ϊ�Խ��������������СΪ
��
��1��������С�����������ʱ������С����ٶȴ�С��
v0������������������ٶȴ�СΪ
v0���������ң�
��2��������С�����������ϵİ�Բ���β۵ĵײ�A��ʱ���Խ����������������
��
����Ϊϵͳ��е���غ㣺
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
�� v1=-
| 1 |
| 2 |
| 1 |
| 2 |
��2��������С��ͨ��A��ʱ���ص��췽�����С�������������й�ͬ�ٶ�v����A�����߷�����ٶ�Ϊv�䣬�ɶ����غ�ͻ�е���غ��
mv0=��m+3m��v
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| 1 |
| 2 |
��� v��=
| ||
| 2 |
��ţ�ٵڶ����ɵ�N=
| mv��2 |
| R |
3m
| ||
| 4R |
��Ϊ�Խ��������������СΪ
3m
| ||
| 4R |
��
��1��������С�����������ʱ������С����ٶȴ�С��
| 1 |
| 2 |
| 1 |
| 2 |
��2��������С�����������ϵİ�Բ���β۵ĵײ�A��ʱ���Խ����������������
3m
| ||
| 4R |

��ϰ��ϵ�д�
 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
�����Ŀ