题目内容
(18分)探究某种笔的弹跳问题时,把笔分为轻质弹簧、内芯和外壳三部分,其中内芯和外壳质量分别为m和4m.笔的弹跳过程分为三个阶段:
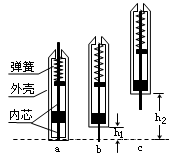
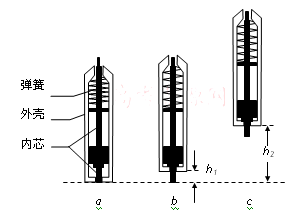
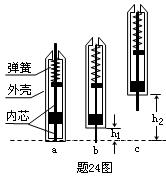
①把笔竖直倒立于水平硬桌面,下压外壳使其下端接触桌面(见图a);
②由静止释放,外壳竖直上升至下端距桌面高度为h1时,与静止的内芯碰撞(见图b);
③碰后,内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度为h2处(见图c)。
设内芯与外壳的撞击力远大于笔所受重力、不计摩擦与空气阻力,重力加速度为g。求:
(1)外壳与内芯碰撞后瞬间的共同速度大小;
(2)从外壳离开桌面到碰撞前瞬间,弹簧做的功;
(3)从外壳下端离开桌面到上升至h2处,笔损失的机械能。
解析:
设外壳上升高度h1时速度为V1,外壳与内芯碰撞后瞬间的共同速度大小为V2,
(1)对外壳和内芯,从撞后达到共同速度到上升至h2处,应用动能定理有
(4mg+m)( h2-h1)=![]() (4m+m)V22,解得V2=
(4m+m)V22,解得V2=![]() ;
;
(2)外壳和内芯,碰撞过程瞬间动量守恒,有4mV1=(4mg+m)V2,
解得V1=![]() ,
,
设从外壳离开桌面到碰撞前瞬间弹簧做功为W,在此过程中,对外壳应用动能定理有
W-4mgh1=![]() (4m)V12,
(4m)V12,
解得W=![]() mg;
mg;
(3)由于外壳和内芯达到共同速度后上升高度h2的过程,机械能守恒,只是在外壳和内芯碰撞过程有能量损失,损失的能量为![]() =
=![]() (4m)V12-
(4m)V12-![]() (4m+m)V22,
(4m+m)V22,
联立解得![]() =
=![]() mg(h2-h1)。
mg(h2-h1)。

练习册系列答案
相关题目
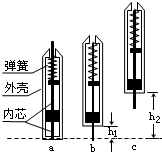
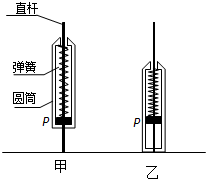 (2010?武汉二模)在探究某种笔的弹跳问题时,建立以下简化模型进行研究.
(2010?武汉二模)在探究某种笔的弹跳问题时,建立以下简化模型进行研究.