题目内容
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示.开始时OA边处于水平位置，由静止释放,则( )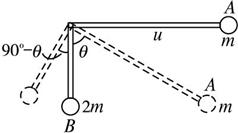
A.A球的最大速度为2
B.A球的速度最大时，两小球的总重力势能最小
C.A球的速度最大时，两直角边与竖直方向的夹角为45°
D.A、B两球的最大速度之比vA∶vB=2∶1
BCD
解析：由机械能守恒可知,两球总重力势能最小时,二者的动能最大,根据题意知两球的角速度相同,线速度之比为vA∶vB=(ω·2l)∶(ω·l)=2∶1,故选项B、D是正确的.当OA与竖直方向的夹角为θ时,由机械能守恒定律得：mg2lcosθ-2mgl(1-sinθ)
=mvB2+
mvA2
可得：vA2=
mgl(sinθ+cosθ)-
mgl.
由数学知识知,当θ=45°时,sinθ+cosθ有最大值,故选项C是正确的.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2003?上海）一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B．支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示．开始时OA边处于水平位置，由静止释放，则（ ）
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B．支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示．开始时OA边处于水平位置，由静止释放，则（ ）
（2011?长宁区一模）一质量不计的直角形支架两端分别连接质量为m和2m的小球A和 B．支架的两直角边长度分别为2l和l，支架可绕固定轴O在竖直平面内转动，如图所示．开始时OA边处于水平位置，由静止释放，不计任何阻力．转动中设OA边与水平方向的夹角为θ，则当A球速度达最大时θ为
（2007?湖南模拟）一质量不计的直角形支架两端分别连接质量均为m的小球A和B．支架的两直角边长度分别为l和2l，支架可绕固定轴O在竖直平面内无摩擦转动，如图所示．开始时OA边处于水平位置，由静止释放，则（ ）