Question

【题目】如图所示，左侧竖直墙面上固定半径为R=0.3m的光滑半圆环，右侧竖直墙面上与圆环的圆心O等高处固定一光滑直杆。质量为ma=1kg的小球a套在半圆环上，质量为mb=0.5kg的滑块b套在直杆上，二者之间用长为l=0.4m的轻杆通过两铰链连接。现将a从圆环的最高处由静止释放，使a沿圆环自由下滑，不计一切摩擦，a、b均视为质点，重力加速度g=10 m/s2。求：

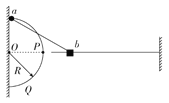
（1）小球a滑到与圆心O等高的P点时的向心力大小；

（2）小球a从P点下滑至杆与圆环相切的Q点的过程中，杆对滑块b做的功。(结果保留一位小数)

Answer 1

【答案】（1）20N；（2）2.4J

【解析】

（1）当a滑到与O同高度P点时，a的速度v沿圆环切向向下，b的速度为零，由机械能守恒定律可得

解得小球a滑到与圆心O等高的P点时的速度

对小球a受力分析，在P点，由牛顿第二定律可得向心力大小

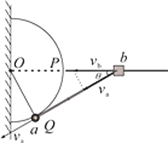
（2）杆与圆相切时，如图所示，a的速度沿杆方向，设此时b的速度为vb，根据杆不可伸长和缩短，有：

va=vbcosθ

由几何关系可得

在图中，从P到Q，球a下降的高度h =Rcosθ，a、b系统机械能守恒，则有

对滑块b，由动能定理解得杆对滑块b做的功

2.4J

答：（1）小球a滑到与圆心O等高的P点时的向心力大小为20N，（2）小球a从P点下滑至杆与圆环相切的Q点的过程中，杆对滑块b做的功为2.4J。