Question

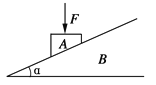
【题目】质量为M，倾角为30°的光滑斜面静止在粗糙的水平地面上，斜面上两个质量分别为m1、m2的小球A、B，它们用劲度系数为k的轻质弹簧连接，现对小球B施加一水平向左的拉力F使A、B及斜面一起向左做匀速直线运动，已知弹簧的原长为L0，重力加速度为g，求：

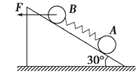
(1)此时弹簧的长度L；

(2)水平拉力F的大小及粗糙地面与斜面体间的动摩擦因素。

Answer 1

【答案】(1) (2)，

【解析】

(1)以球A为研究对象，受力分析后根据平衡条件列式求解弹簧弹力，然后结合胡克定律列式求解弹簧的伸长量和长度；

(2)以A、B及弹簧整体为研究对象，受力分析后根据平衡条件列式求解；

(3)以A、B、斜面及弹簧整体为研究对象，受力分析后根据共点力平衡条件列式求解摩擦力和支持力，最后根据滑动摩擦定律列式求解动摩擦因数。

(1) 以A为研究对象，受重力、拉力和支持力，根据平衡条件，有：

k（L-L0）= m1gsin30°

解得：L=；

(2) 以A、B及弹簧整体为研究对象，受拉力、滑动摩擦力、重力和支持力，根据平衡条件，有：

Fcos30°=

解得：

以A、B、斜面及弹簧整体为研究对象，根据平衡条件，有：

F=f=μ（M+m1+m2）g

解得： 。