Question

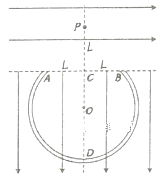
【题目】如图所示，一内壁光滑的绝缘圆管ADB固定在竖直平面内，圆管的圆心为0，D点为圆管的最低点，A、B两点在同一水平线上，AB＝2L，圆环的半径rL（圆管的直径忽略不计），过OD的虚线与过AB的虚线垂直相交于C点，在虚线AB的上方存在水平向右的、范围足够大的匀强电场；虚线AB的下方存在竖直向下的、范围足够大的匀强电场，电场强度大小等于，圆心0正上方的P点有一质量为m、电荷量为﹣q（q＞0）的绝缘小物体（可视为质点），PC间距为L．现将该小物体无初速度释放，经过一段时间，小物体刚好沿切线无碰撞地进入圆管内，并继续运动，重力加速度用g表示。

（1）虚线AB上方匀强电场的电场强度为多大？

（2）小物体到达A点时速度的大小？

（3）小物体由P点运动到B点的时间为多少？

Answer 1

【答案】（1）；（2）2，（3）（1）；

【解析】

小物体释放后在重力和电场力的作用下做匀加速直线运动，根据正交分解，垂直运动方向的合力为零，列出平衡方程即可求出虚线AB上方匀强电场的电场强度；从P到A的过程中，根据动能定理可求得小物体到达A点时速度的大小；利用匀变速直线运动的规律求解粒子做匀加速直线运动的时间t1，再根据圆周运动规律物体在圆管内做匀速圆周运动的时间为t2，两时间之和即为由P到B的总时间。

（1）小物体在重力和电场力的作用下做匀加速直线运动，小物体从A点切线方向进入，

则此时速度方与竖直方向的夹角为45°，即加速度方向与竖直方向的夹角为45°，

则有：tan45°

解得：E

（2）从P到A的过程中，根据动能定理得：mgL+EqLmv2A﹣0

解得：vA＝2，

（3）小物体从B点抛出后做类平抛运动，小物体的加速度：ag

小物体由P点运动到A点做匀加速直线运动，设所用时间为t1

则有：Lgt12

解得：t1

物体在圆管内做匀速圆周运动的时间t2，则：t2

总时间为：t总＝（1）