题目内容
5.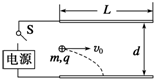 如图所示,水平放置的平行板电容器与某一电源相连,它的极板长L=0.4m,两极板间距离d=4×10-3 m,有一束由相同带电微粒组成的粒子流以相同的速度v0从两极板中央平行极板射入,开关S闭合前,两极板间不带电,由于重力作用,微粒能落到下极板的正中央.已知微粒质量m=4×10-5 kg、电荷量q=+1×10-8 C,g=10m/s2,则下列说法正确的是( )
如图所示,水平放置的平行板电容器与某一电源相连,它的极板长L=0.4m,两极板间距离d=4×10-3 m,有一束由相同带电微粒组成的粒子流以相同的速度v0从两极板中央平行极板射入,开关S闭合前,两极板间不带电,由于重力作用,微粒能落到下极板的正中央.已知微粒质量m=4×10-5 kg、电荷量q=+1×10-8 C,g=10m/s2,则下列说法正确的是( )| A. | 微粒的入射速度v0=10 m/s | |
| B. | 电容器上板接电源正极时微粒有可能从平行板电容器的右边射出电场 | |
| C. | 电源电压为160 V时,微粒可能从平行板电容器的右边射出电场 | |
| D. | 电源电压为100 V时,微粒可能从平行板电容器的右边射出电场 |
分析 (1)粒子刚进入平行板时,两极板不带电,粒子做的是平抛运动,根据平抛运动的规律可以求得粒子入射速度v0的大小;
(2)由于两板之间加入了匀强电场,此时带电粒子在电场中的运动是类平抛运动,仍把运动在水平和竖直两个方向上分解,进行列式计算.由于带电粒子的水平位移增加,在板间的运动时间变大,而竖直方向位移不变,所以在竖直方向的加速度减小了,由此可判断受到了竖直向上的电场力作用,再结合牛顿运动定律列式求解即可.
解答 解:A、粒子刚进入平行板时,两极板不带电,粒子做的是平抛运动,则有:
水平方向有$\frac{L}{2}$=v0t
竖直方向有$\frac{d}{2}$=$\frac{1}{2}$gt2,
解得 v0=10m/s,所以A正确;
B、由于带电粒子的水平位移增加,在板间的运动时间变大,而竖直方向位移不变,所以在竖直方向的加速度减小,所以电场力方向向上,又因为是正电荷,所以上极板与电源的负极相连,所以B错误;
C、当所加电压为U时,微粒恰好从下板的右边缘射出,则有:
水平方向有L=v0t′
竖直方向有$\frac{d}{2}$=$\frac{1}{2}$at′2,
解得:a=2.5m/s2;
根据牛顿第二定律得:a=$\frac{mg-q\frac{U}{d}}{m}$ 解得:U=120V,
若微粒恰好从上板的右边缘射出,则有:
根据牛顿第二定律得:a=$\frac{q\frac{U}{d}-mg}{m}$ 解得:U=200V,所以C正确,D错误.
故选:AC.
点评 解得此类问题,首先要正确的对带电粒子在这两种情况下进行正确的受力分析,确定粒子的运动类型.解决带电粒子垂直射入电场的类型的题,应用平抛运动的规律进行求解.
此类型的题要注意是否要考虑带电粒子的重力,原则是:除有说明或暗示外,对基本粒子(例如电子,质子、α粒子、离子等),一般不考虑重力;对带电微粒,(如液滴、油滴、小球、尘埃等),一般要考虑重力.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | 胡克发现了弹簧弹力与弹簧形变量的关系 | |
| B. | 开普勒以行星运动定律为基础总结出万有引力定律 | |
| C. | 牛顿提出了万有引力定律,并通过实验测出了引力常量 | |
| D. | 伽利略在前人的基础上通过观察总结得到行星运动三定律 |
| A. | 它们做圆周运动所需要的向心力由太阳对它们的引力提供 | |
| B. | 它们中质量较大的星的向心力较大 | |
| C. | 它们做圆周运动的线速度大小之比与其质量成反比 | |
| D. | 它们做圆周运动的角速度之比与其质量成反比 |
| A. | 天文学家研究$\underset{地}{•}$$\underset{球}{•}$的自转 | |
| B. | 教练员对$\underset{短}{•}$$\underset{跑}{•}$$\underset{运}{•}$$\underset{动}{•}$$\underset{员}{•}$的起跑动作进行指导 | |
| C. | 用GPS确定$\underset{远}{•}$$\underset{洋}{•}$$\underset{海}{•}$$\underset{轮}{•}$在大海中的位置 | |
| D. | 在国际大赛中,乒乓球运动员王浩准备接对手发出的$\underset{旋}{•}$$\underset{转}{•}$$\underset{球}{•}$ |
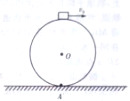
| A. | 若v0=$\sqrt{gR}$,则物块落地点离A点距离为$\sqrt{2R}$ | |
| B. | 若球面是粗糙的,当v0<$\sqrt{gR}$时,物块一定会沿球面下滑一段 | |
| C. | 若v0<$\sqrt{gR}$,则物块落地点离A点距离为R | |
| D. | 若v0≥$\sqrt{gR}$,则物块落地点离A点至少为2R |
| A. | 当研究护航舰艇的运行轨迹时,能将其看做质点 | |
| B. | “5000多海里”指的是护航舰艇的航行位移 | |
| C. | 根据题中数据不能大约求出护航舰艇的平均速度 | |
| D. | 题中数据“4月3日上午10时”和“4月21日晨”指的是时刻 |
| A. | 有的物体内部有电荷,有的物体内部没有电荷,所以有带电的物体,也有不带电的物体 | |
| B. | 物体不带电是因为所带的正电荷数目和负电荷数目相等 | |
| C. | 自然界只有两种电荷,点电荷和元电荷 | |
| D. | 我们可以通过某一种方式创造电荷 |
 一只松鼠静止地站在倾斜的树枝上,一只猴子从树枝上朝向右上方由静止跳出,则树枝对松鼠和猴子的弹力方向为( )
一只松鼠静止地站在倾斜的树枝上,一只猴子从树枝上朝向右上方由静止跳出,则树枝对松鼠和猴子的弹力方向为( )| A. | 树枝对松鼠没有弹力 | B. | 树枝对松鼠弹力竖直向下 | ||
| C. | 树枝对猴子弹力垂直树干斜向上 | D. | 树枝对猴子弹力竖直向上 |
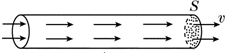 证明电流的微观表达式.有一横截面积为S的铜导线,单位体积内的自由电子数为n,自由电子定向移动的速率为v,如果电子的电荷量为e.
证明电流的微观表达式.有一横截面积为S的铜导线,单位体积内的自由电子数为n,自由电子定向移动的速率为v,如果电子的电荷量为e.