题目内容
4.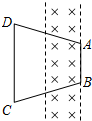 如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合,AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.先让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )
如图所示,平行虚线之间有垂直于纸面向里的匀强磁场,磁场左右宽度为L,磁感应强度大小为B.一等腰梯形线圈ABCD所在平面与磁场垂直,AB边刚好与磁场右边界重合,AB长等于L,CD长等于2L,AB、CD间的距离为2L,线圈的电阻为R.先让线圈向右以恒定速度v匀速运动,从线圈开始运动到CD边刚好要进入磁场的过程中( )| A. | 线圈中感应电流沿逆时针方向 | B. | 线圈中感应电动势大小为BLv | ||
| C. | 通过线圈截面的电量为$\frac{B{L}^{2}}{R}$ | D. | 线圈克服安培力做的功为$\frac{{B}^{2}{L}^{2}v}{4R}$ |
分析 当线圈向右运动时穿过线圈的磁通量增加,根据楞次定律判断感应电流的方向.根据公式E=BLv,L是有效切割长度,求解感应电动势.根据q=$\frac{△Φ}{R}$求解电量.克服安培力做的功等于线圈产生的焦耳热.
解答 解:A、当线圈向右运动时穿过线圈的磁通量在增加,根据楞次定律判断知,感应电流沿逆时针方向,故A正确.
B、设∠ADC=θ,由几何知识可得:cotθ=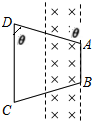 $\frac{\frac{L}{2}}{2L}$=$\frac{1}{4}$.磁场左右宽度为L,线圈有效的切割长度为
$\frac{\frac{L}{2}}{2L}$=$\frac{1}{4}$.磁场左右宽度为L,线圈有效的切割长度为
2Lcotθ=$\frac{L}{2}$
所以线圈中感应电动势大小为 E=B•$\frac{L}{2}$v=$\frac{1}{2}$BLv.故B错误.
C、通过线圈截面的电量为 q=$\frac{△Φ}{R}$=$\frac{B•(\frac{2L+\frac{3}{2}L}{2}•L-\frac{\frac{3}{2}L+L}{2}•L)}{R}$=$\frac{B{L}^{2}}{2R}$,故C错误.
D、由B项分析知线圈产生的感应电动势不变,克服安培力做的功等于线圈产生的焦耳热,则克服安培力做的功为 W=$\frac{{E}^{2}}{R}$t=$\frac{(\frac{1}{2}BLv)^{2}}{R}$$•\frac{L}{v}$=$\frac{{B}^{2}{L}^{2}v}{4R}$.故D正确.
故选:AD.
点评 解决本题的关键要正确理解感应电动势公式E=BLv中L的含义,知道L是有效切割长度,即与线圈速度垂直的导线长度.由于是选择题,感应电荷量公式q=$\frac{△Φ}{R}$可以直接运用.

练习册系列答案
相关题目
14.甲、乙、丙为三颗地球卫星,其中甲为地球同步卫星,乙和丙在同一个轨道一前一后(乙在前丙在后)且运行高度低于甲的运行高度,三卫星轨道均可视为圆轨道.下列判断正确的是( )
| A. | 甲的周期小于丙的周期 | |
| B. | 甲的加速度小于乙的加速度 | |
| C. | 甲在运行时能经过北极的正上方 | |
| D. | 丙要想追上乙可以通过增大速度来实现 |
19.起跳摸高是同学们经常进行的一项活动.某学生身高1.80m,质量70kg,他站立举臂,手指摸到的高度为2.10m,在一次摸高测试中,如果他先下蹲,再用力蹬地向上跳起,同时举臂,离地后手指摸到的高度为2.55 m.设他从蹬地到离开地面所用的时间为0.7 s.不计空气阻力(取g=10 m/s2).该同学跳起后增加的重力势能最大值是( )
| A. | 1260J | B. | 1470J | C. | 315J | D. | 1785J |
5.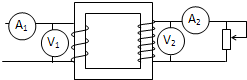 一理想变压器给负载供电,变压器输入电压不变,如图所示.如果负载电阻的滑片向上移动则图中所有交流电表的读数及输入功率变化情况正确的是(均为理想电表)( )
一理想变压器给负载供电,变压器输入电压不变,如图所示.如果负载电阻的滑片向上移动则图中所有交流电表的读数及输入功率变化情况正确的是(均为理想电表)( )
 一理想变压器给负载供电,变压器输入电压不变,如图所示.如果负载电阻的滑片向上移动则图中所有交流电表的读数及输入功率变化情况正确的是(均为理想电表)( )
一理想变压器给负载供电,变压器输入电压不变,如图所示.如果负载电阻的滑片向上移动则图中所有交流电表的读数及输入功率变化情况正确的是(均为理想电表)( )| A. | V1、V2不变,A1增大,A2减少,P增大 | B. | V1、V2不变,A1、A2增大,P增大 | ||
| C. | V1、V2不变,A1、A2减少,P减少 | D. | V1不变、V2增大,A1、A2减少,P减少 |
12.关于“探究功与速度变化的关系”的实验中,下面的说法中有一项不正确,它是( )
| A. | 本实验设法让橡皮筋对小车做的功分别为W、2W、3W、….所采用的方法是选用同样的橡皮筋,并在每次实验中使橡皮筋拉伸的长度保持一致.当用l条橡皮筋进行是实验时,橡皮筋对小车做的功为W,用2条、3条、…橡皮筋并在一起进行第2次、第3次…实验时,橡皮筋对小车做的功分别是2W、3W、… | |
| B. | 小车运动中会受到阻力,补偿的方法,可以使木板适当倾斜 | |
| C. | 某同学在一次实验中,得到一条记录纸带.纸带上打出的点,两端密、中间疏.出现这种情况的原因,可能是没有使木板倾斜或倾角太小 | |
| D. | 根据记录纸带上打出的点,求小车获得的速度的方法,是以纸带上第一点到最后一点的距离来进行计算 |
9.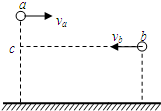 如图所示,从地面上方不同高度处以水平速度va、vb抛出两小球a、b,结果a落在b初始位置的正下方,而b落在a初始位置的正下方,bc为过小球b初始位置的水平线,不计空气阻力,下列判断正确的有( )
如图所示,从地面上方不同高度处以水平速度va、vb抛出两小球a、b,结果a落在b初始位置的正下方,而b落在a初始位置的正下方,bc为过小球b初始位置的水平线,不计空气阻力,下列判断正确的有( )
 如图所示,从地面上方不同高度处以水平速度va、vb抛出两小球a、b,结果a落在b初始位置的正下方,而b落在a初始位置的正下方,bc为过小球b初始位置的水平线,不计空气阻力,下列判断正确的有( )
如图所示,从地面上方不同高度处以水平速度va、vb抛出两小球a、b,结果a落在b初始位置的正下方,而b落在a初始位置的正下方,bc为过小球b初始位置的水平线,不计空气阻力,下列判断正确的有( )| A. | 两球抛出时的初速度va>vb | |
| B. | 若两小球同时抛出,它们可能在空中相遇 | |
| C. | 若两小球同时抛出,它们不能在空中相遇 | |
| D. | 若要使它们能在空中相遇,必须在a到达bc时将b抛出 |
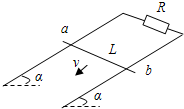 如图所示,宽度为L=1m的导轨与水平面成37°角倾斜放置,上端串接一个阻值为1Ω的定值电阻R,导体棒ab的电阻为r=0.5Ω,质量为0.1kg.其余电阻不计.空间有垂直导轨平面的匀强磁场,磁感应强度B=0.4T.已知,导体棒从静止开始下滑,能达到的最大速度为5m/s,(sin37°=0.6,Cos37°=0.8)求
如图所示,宽度为L=1m的导轨与水平面成37°角倾斜放置,上端串接一个阻值为1Ω的定值电阻R,导体棒ab的电阻为r=0.5Ω,质量为0.1kg.其余电阻不计.空间有垂直导轨平面的匀强磁场,磁感应强度B=0.4T.已知,导体棒从静止开始下滑,能达到的最大速度为5m/s,(sin37°=0.6,Cos37°=0.8)求