题目内容
18.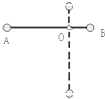 如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为mA=$\frac{1}{2}$mB=m,轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动.当轻杆转至水平位置时,A球速度为$\sqrt{\frac{2}{3}gl}$,则在以后的运动过程中( )
如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为mA=$\frac{1}{2}$mB=m,轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动.当轻杆转至水平位置时,A球速度为$\sqrt{\frac{2}{3}gl}$,则在以后的运动过程中( )| A. | A、B球系统机械能守恒 | |
| B. | 当B球运动至最低点时,球A对杆作用力等于0 | |
| C. | 当B球运动到最高点时,杆对B球作用力等于$\frac{mg}{2}$ | |
| D. | A、B球两球均做匀速圆周运动 |
分析 以O为支点时系统的力矩恰好平衡,说明是匀速圆周运动,根据向心力公式求解出需要的向心力,比较其与重力的关系来得出杆的弹力情况,结合动能定理分析弹力做功情况.
解答 解:A、对于A、B系统只有重力做功,机械能守恒,故A正确;
BD、由题目条件可知两球重力相对于O的力矩平衡,说明两球做匀速圆周运动;A、B两个球的角速度相等,转动半径之比为2:1,根据v=rω,故A、B两个球的线速度之比为2:1;当B球运动至最低点,A球运动至最高点时,由于A的向心力 F向A=m$\frac{{v}_{A}^{2}}{\frac{2}{3}l}$=m$\frac{(\sqrt{\frac{2}{3}gl})^{2}}{\frac{2}{3}l}$=mg,由牛顿第二定律可知此时轻杆对球A作用力等于0,则球A对杆的作用力为0.故BD正确;
C、当B球运动到最高点时速度为vB=$\frac{1}{2}$$\sqrt{\frac{2}{3}gl}$,向心力F向B=(2m)$\frac{{v}_{B}^{2}}{\frac{1}{3}l}$=mg<mBg;故杆对B球作用力为支持力;根据牛顿第二定律得:2mg-N=F向B,N=mg,故C错误;
故选:ABD.
点评 本题关键是知道两个球的机械能均不守恒,是两个球系统的机械能守恒,同时要结合向心力公式列式求解需要的向心力,比较其与重力的大小关系来判断有无弹力.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.汽车以24m/s的速度做匀速直线运动,刹车后的加速度大小为4m/s2,那么开始刹车后2s与开始刹车后8s汽车通过的位移之比为( )
| A. | 7:16 | B. | 5:9 | C. | 3:4 | D. | 4:3 |
6.同步卫星相对于地面静止不动,犹如悬在空中一样,下列说法正确的是( )
| A. | 同步卫星处于平衡状态 | |
| B. | 同步卫星绕地心的角速度跟地球自转的角速度相等 | |
| C. | 同步卫星只能位于赤道上方 | |
| D. | 同步卫星的高度和速率是唯一确定的 |
13. 两实验小组使用相同规格的元件,按图所示电路进行测量.他们将滑动变阻器的滑片P分别置于a、b、c、d、e五个间距相同的位置(a、e为滑动变阻器的两个端点),把相应的电流表示数记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.
两实验小组使用相同规格的元件,按图所示电路进行测量.他们将滑动变阻器的滑片P分别置于a、b、c、d、e五个间距相同的位置(a、e为滑动变阻器的两个端点),把相应的电流表示数记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.
表一(第一实验组)
表二(第二实验组)
滑动变阻器发生断路的是第二实验组;断路发生在滑动变阻器d-e段.
 两实验小组使用相同规格的元件,按图所示电路进行测量.他们将滑动变阻器的滑片P分别置于a、b、c、d、e五个间距相同的位置(a、e为滑动变阻器的两个端点),把相应的电流表示数记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.
两实验小组使用相同规格的元件,按图所示电路进行测量.他们将滑动变阻器的滑片P分别置于a、b、c、d、e五个间距相同的位置(a、e为滑动变阻器的两个端点),把相应的电流表示数记录在表一、表二中.对比两组数据,发现电流表示数的变化趋势不同.经检查,发现其中一个实验组使用的滑动变阻器发生断路.表一(第一实验组)
| P的位置 | a | b | c | d | E | |
| A的示数(A) | 0.84 | 0.48 | 0.42 | 0.48 | 0.84 |
| P的位置 | a | b | c | d | X | e |
| A的示数(A) | 0.84 | 0.42 | 0.28 | 0.21 | 0.84 |
10.(多选)下列说法中正确的是( )
| A. | 用不可见光照射金属一定比用可见光照射同种金属产生的光电子的初动能大 | |
| B. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,但原子的能量增大 | |
| C. | “探究碰撞中的不变量”的实验中得到的结论是碰撞前后两个物体mv的矢量和保持不变 | |
| D. | 在光照条件不变的情况下,对发射出来的光电子加上正向电压对光电子加速,所加电压不断增大,光电流也不断增大 |
7.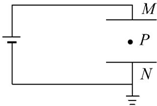 如图所示,两块正对平行金属板M、N与电池相连,N板接地,在距两板等距离的P点固定一个带正电的点电荷,如果M板向上平移一小段距离,则( )
如图所示,两块正对平行金属板M、N与电池相连,N板接地,在距两板等距离的P点固定一个带正电的点电荷,如果M板向上平移一小段距离,则( )
 如图所示,两块正对平行金属板M、N与电池相连,N板接地,在距两板等距离的P点固定一个带正电的点电荷,如果M板向上平移一小段距离,则( )
如图所示,两块正对平行金属板M、N与电池相连,N板接地,在距两板等距离的P点固定一个带正电的点电荷,如果M板向上平移一小段距离,则( )| A. | 点电荷受到的电场力减小 | B. | M板的带电量增加 | ||
| C. | P点的电势升高 | D. | 点电荷在P点具有的电势能增加 |
8.下列说法正确的是( )
| A. | 光的干涉和衍射说明光是机械波 | |
| B. | 当波源与观察者相互远离时,观察到的频率变大 | |
| C. | 光的偏振现象说明光是横波 | |
| D. | 用光导纤维传播信号,利用了光的衍射 |
 如图所示,质量均为km(其中k=1,2,3…)的斜劈A和B静止放在光滑的水平面上,斜劈A和B的曲面为半径相同的四分之一的圆周,圆周下端与水平面相切,一质量为m的小球位于两斜劈的中间某位置,现给小球水平向右的初速度v0,求:
如图所示,质量均为km(其中k=1,2,3…)的斜劈A和B静止放在光滑的水平面上,斜劈A和B的曲面为半径相同的四分之一的圆周,圆周下端与水平面相切,一质量为m的小球位于两斜劈的中间某位置,现给小球水平向右的初速度v0,求: