题目内容
9. 如图所示,质量均为km(其中k=1,2,3…)的斜劈A和B静止放在光滑的水平面上,斜劈A和B的曲面为半径相同的四分之一的圆周,圆周下端与水平面相切,一质量为m的小球位于两斜劈的中间某位置,现给小球水平向右的初速度v0,求:
如图所示,质量均为km(其中k=1,2,3…)的斜劈A和B静止放在光滑的水平面上,斜劈A和B的曲面为半径相同的四分之一的圆周,圆周下端与水平面相切,一质量为m的小球位于两斜劈的中间某位置,现给小球水平向右的初速度v0,求:(1)若将斜劈B固定,小球刚好滑到斜劈顶端,斜劈的半径多大;
(2)若两斜劈均不固定,当小球第一次从斜劈B滑下离开时,小球的速度多大;
(3)在满足(2)问前提下,若小球至少2次向右滑上斜劈B,k的取值范围.
分析 (1)应用动能定理可以求出斜劈的半径.
(2)系统动量守恒,由动量守恒定律与机械能守恒定律求出速度.
(3)由动量守恒定律求出速度,然后根据题意确定k的值
解答 解:(1)斜劈B固定,小球刚好滑到斜劈顶端,
小球运动过程,由动能定理得:-mgR=0-$\frac{1}{2}$mv02,
解得,斜劈的半径:R=$\frac{{v}_{0}^{2}}{2g}$;
(2)设小球第一次从斜劈B滑下离开时,小球和斜劈B的速度分别为v1和v2,
以向右为正方向,由动量守恒可得:mv0=mv1+kmv2,
由机械能守恒可得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$kmv22,
联立解得小球速度为:v1=$\frac{1-k}{1+k}$v0,斜劈B速度为:v2=$\frac{2}{1+k}$v0;
(3)设小球第一次滑下离开斜劈A时,小球和斜劈A的速度分别为v1′和v2′,
以向右为正方向,由动量守恒可得:mv0=mv1+kmv2,联立解得小球的速度:v1′=$\frac{1-k}{1+k}$v1=$(\frac{1-k}{1+k})^{2}$v0,
若小球至少两次向右滑上斜劈B,则必有:|v1′|>v2,化简得:k2-4k-1>0,
解得:k>2+$\sqrt{5}$,故k=5、6、7、…;
答:(1)若将斜劈B固定,小球刚好滑到斜劈顶端,斜劈的半径为$\frac{{v}_{0}^{2}}{2g}$;
(2)若两斜劈均不固定,当小球第一次从斜劈B滑下离开时,小球的速度为$\frac{1-k}{1+k}$v0;
(3)在满足(2)问前提下,若小球至少2次向右滑上斜劈B,k的取值范围是:k=5、6、7、….
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与机械能守恒定律即可正确解题.

 阅读快车系列答案
阅读快车系列答案
| A. | 前5s的平均速度是0.5m/s | |
| B. | 前10s钢索最容易发生断裂 | |
| C. | 30s~36s钢索拉力的功率不变 | |
| D. | 0~10s的平均速度等于30s~36s的平均速度 |
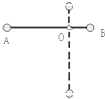 如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为mA=$\frac{1}{2}$mB=m,轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动.当轻杆转至水平位置时,A球速度为$\sqrt{\frac{2}{3}gl}$,则在以后的运动过程中( )
如图所示,轻杆AB长l,两端各连接一个小球(可视为质点),两小球质量关系为mA=$\frac{1}{2}$mB=m,轻杆绕距B端$\frac{l}{3}$处的O轴在竖直平面内顺时针自由转动.当轻杆转至水平位置时,A球速度为$\sqrt{\frac{2}{3}gl}$,则在以后的运动过程中( )| A. | A、B球系统机械能守恒 | |
| B. | 当B球运动至最低点时,球A对杆作用力等于0 | |
| C. | 当B球运动到最高点时,杆对B球作用力等于$\frac{mg}{2}$ | |
| D. | A、B球两球均做匀速圆周运动 |
 在验证机械能守恒定律的实验中,质量为0.20kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示.已知相邻计数点间的时间间隔为0.02秒,当地的重力加速度为9.80m/s2,回答以下问题.
在验证机械能守恒定律的实验中,质量为0.20kg的重物拖着纸带自由下落,在纸带上打出一系列的点,如图所示.已知相邻计数点间的时间间隔为0.02秒,当地的重力加速度为9.80m/s2,回答以下问题. 放在水平地面上的一物块处于静止状态,受到方向不变的水平推力F的作用,F的大小与时间t的关系如图甲所示;物块的运动速度v与时间t的关系如图乙所示,6s后的速度图象没有画出,9s后撤去外力F,g取10m/s2.求:
放在水平地面上的一物块处于静止状态,受到方向不变的水平推力F的作用,F的大小与时间t的关系如图甲所示;物块的运动速度v与时间t的关系如图乙所示,6s后的速度图象没有画出,9s后撤去外力F,g取10m/s2.求: 在“探究小车速度随时间变化的规律”的实验中,得到一条纸带如图所示,A、B、C、D、E、F为相邻的6个计数点,若相邻两计数点的时间间隔为0.1s,则粗测小车的加速度为1.58m/s2,B点的瞬时速度为0.359m/s.
在“探究小车速度随时间变化的规律”的实验中,得到一条纸带如图所示,A、B、C、D、E、F为相邻的6个计数点,若相邻两计数点的时间间隔为0.1s,则粗测小车的加速度为1.58m/s2,B点的瞬时速度为0.359m/s. 如图所示,竖直放置的U形管,左端封闭右端开口,管内水银将长19cm的空气柱封在左管内,此时两管内水银面的高度差为4cm,大气压强为标准大气压.现向右管内再注入水银,使空气柱长度减少1cm,若温度保持不变,则需注入水银柱的长度为多少?
如图所示,竖直放置的U形管,左端封闭右端开口,管内水银将长19cm的空气柱封在左管内,此时两管内水银面的高度差为4cm,大气压强为标准大气压.现向右管内再注入水银,使空气柱长度减少1cm,若温度保持不变,则需注入水银柱的长度为多少?