Question

【题目】如图所示，在相距L=0.5m的两条水平放置无限长的金属导轨上，放置两根金属棒ab和cd，两棒的质量均为m=0.1kg，电阻均为r=1Ω，整个装置处于无限大、竖直向下的匀强磁场中，磁感应强度B=1T，导轨电阻及摩擦力均不计．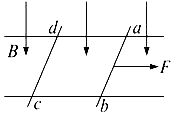

（1）若将cd固定不动，从0时刻起，用一水平向右的拉力F的以恒定功率P=2W作用在ab棒上，使ab棒从静止开始运动，经过t=2.2s时ab棒已达到稳定速度，求此过程中cd棒产生的热量Q？．
（2）若从t=0时刻开始，用一水平向右的恒力F作用于ab棒上，使ab棒从静止开始运动，经过t=4s，回路达到了稳定状态，此后回路中电流保持0.6A不变．求第4秒末
①cd棒的加速度大小及ab棒与cd棒的速度之差；
②ab棒的速度大小．

Answer 1

【答案】
（1）解：由P=Fv可知，拉力大小：F= = ，

ab棒受到的安培力：

F安培=BIL= = =0.125v，

导体棒匀速运动时达到稳定，

由平衡条件得： =0.125v，

解得：v=4m/s，

两导体棒串联且电阻相等，它们产生的热量相等，

由能量守恒定律得：Pt=2Q+ mv2，

解得：Q=1.8J；

答：此过程中cd棒产生的热量Q为1.8J；

（2）①对cd棒，由牛顿第二定律得：

a= = = =3m/s2．

感应电流：I= = = ，

速度之差：△v= = =2.4 m/s；

②回路达到稳定状态，两棒有共同的加速度，

对ab棒，由牛顿第二定律得：F﹣Fcd=ma，解得：F=0.6N，

根据动量定理得：

对ab棒：（F﹣BIL）t=mvab，

对于cd棒：BLIt=mvcd，

整理得：Ft=mvab+mvcd，

解得：vab=13.2 m/s．

答：①第4秒末，cd棒的加速度大小为3m/s2，ab棒与cd棒的速度之差为2.4m/s；

②第4秒末，ab棒的速度大小为13.2m/s．

【解析】（1）当导体棒做匀速直线运动时，代表物体所受合外力为零，对导体棒进行受力分析，根据平衡方程列式求解。
（2）①根据安培力结合牛顿第二运动定律列式求解即可。
②当两棒之间速度之差稳定时，用牛顿第二定律，结合动量定理联立求解。