题目内容
(2011?太原模拟)(1)如图甲所示,O点为振源.OP距离为s.t=0时刻,O点从平衡位置开始向下负方向)振动,产生向右沿直线传播的简谐横波,图乙为P点的振动图象(从t1时刻开始振动).则
A.该波的频率为
B.t2时刻P点的速度最大,方向沿y正方向
C.这列波的波长为
D.若t2时刻O点处于负最大位移处,则s可能是波长的
倍
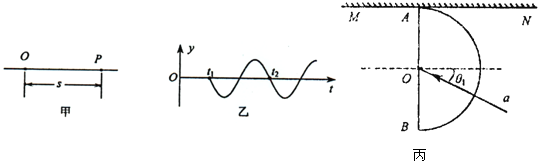
(2)如图丙所示,半圆形玻璃砖的半径R=10cm,折射率n=
,直径AB与屏MN垂直并接触于A点,一细束单色光a以入射角θ1=30°沿半径射向玻璃砖的圆心O,在屏MN上出现了两个光斑.求这两个光斑间的距离L.
AC
AC
.(填入正确选项前的字母)
A.该波的频率为
| 1 |
| t2-t1 |
B.t2时刻P点的速度最大,方向沿y正方向
C.这列波的波长为
| s(t2-t1) |
| t1 |
D.若t2时刻O点处于负最大位移处,则s可能是波长的
| 3 |
| 4 |
(2)如图丙所示,半圆形玻璃砖的半径R=10cm,折射率n=
| 3 |
分析:(1)由题,OP距离为s,P点从t1时刻开始振动,由v=
求出波速.由乙图读出周期,求出频率和波长.结合波形分析若t2时刻O点处于负最大位移处,s与波长的关系.
(2)画出光路图,由折射定律求出折射角,根据几何知识求出这两个光斑间的距离L.
| s |
| t1 |
(2)画出光路图,由折射定律求出折射角,根据几何知识求出这两个光斑间的距离L.
解答:解: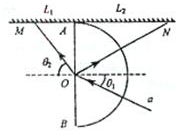
(1)A、由乙图读出该波的周期为T=t2-t1,则其频率为f=
=
.故A正确.
B、t2时刻P点位于平衡位置,速度最大,而且沿y轴负方向.故B错误.
C、由题得到该波的波速为v=
,则波长为λ=vT=
.故C正确.
D、若t2时刻O点处于负最大位移处,而此时刻t2时刻P点位于平衡位置沿y轴负方向,结合波形分析可知,s可能是波长的
倍.故D错误.
故选AC
(2)作出光路图如图所示.根据折射定律得:
=
,其中θ1=30°,n=
,代入解得,θ2=60°.
根据几何知识得到:两个光斑间的距离L=Rtan30°+Rtan60°
代入解得,L≈0.23m.
故答案为:
(1)AC
(2)两个光斑间的距离是0.23m.

(1)A、由乙图读出该波的周期为T=t2-t1,则其频率为f=
| 1 |
| T |
| 1 |
| t2-t1 |
B、t2时刻P点位于平衡位置,速度最大,而且沿y轴负方向.故B错误.
C、由题得到该波的波速为v=
| s |
| t1 |
| s(t2-t1) |
| t1 |
D、若t2时刻O点处于负最大位移处,而此时刻t2时刻P点位于平衡位置沿y轴负方向,结合波形分析可知,s可能是波长的
| 1 |
| 4 |
故选AC
(2)作出光路图如图所示.根据折射定律得:
| sinθ1 |
| sinθ2 |
| 1 |
| n |
| 3 |
根据几何知识得到:两个光斑间的距离L=Rtan30°+Rtan60°
代入解得,L≈0.23m.
故答案为:
(1)AC
(2)两个光斑间的距离是0.23m.
点评:对于机械波的问题,常常画出波形,分析两质点的状态关系,确定它们之间距离与波长的关系.对于几何光学,作出光路图是解题的基础.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 (2011?太原模拟)如图为一攀岩运动员正沿竖直岩壁缓慢攀登,由于身背较重的行囊,重心上移至肩部的0点,总质量为60kg.此时手臂与身体垂直,手臂与岩壁夹角为53°.则手受到的拉力和脚受到的作用力分别为(设手、脚受到的作用力均通过重心O,g取10m/s2,sin53°=0.8,cos53°=0.6)( )
(2011?太原模拟)如图为一攀岩运动员正沿竖直岩壁缓慢攀登,由于身背较重的行囊,重心上移至肩部的0点,总质量为60kg.此时手臂与身体垂直,手臂与岩壁夹角为53°.则手受到的拉力和脚受到的作用力分别为(设手、脚受到的作用力均通过重心O,g取10m/s2,sin53°=0.8,cos53°=0.6)( ) (2011?太原模拟)为了测量运动员跃起的高度,可在弹性网上安装压力传感器,利用传感器记录运动员运动过程中对弹性网的压力,并由计算机作出压力-时间图象,如图所示.运动员在空中运动时可视为质点,则可求运动员跃起的最大高度为(g取10m/s2)( )
(2011?太原模拟)为了测量运动员跃起的高度,可在弹性网上安装压力传感器,利用传感器记录运动员运动过程中对弹性网的压力,并由计算机作出压力-时间图象,如图所示.运动员在空中运动时可视为质点,则可求运动员跃起的最大高度为(g取10m/s2)( ) (2011?太原模拟)如图所示,在离地面高为H处以水平速度v0抛出一质量为m的小球,经时间t,小球离水平地面的高度变为h,此时小球的动能为EK,重力势能为EP(选水平地面为零势能参考面).下列图象中大致能反映小球动能Ek、势能EP变化规律的是( )
(2011?太原模拟)如图所示,在离地面高为H处以水平速度v0抛出一质量为m的小球,经时间t,小球离水平地面的高度变为h,此时小球的动能为EK,重力势能为EP(选水平地面为零势能参考面).下列图象中大致能反映小球动能Ek、势能EP变化规律的是( ) (2011?太原模拟)如图所示,质量为m=10kg的两个相同的物块A、B(它们之间用轻绳相连)放在水平地面上,在方向与水平方面成θ=37°角斜向上、大小为100N的拉力F作用下,以大小为v0=4.0m/s的速度向右做匀速直线运动,求剪断轻绳后物块A在水平地面上滑行的距离.(取当地的重力加速度(g=10m/s2,sin37°=0.6,cos37°=0.8)
(2011?太原模拟)如图所示,质量为m=10kg的两个相同的物块A、B(它们之间用轻绳相连)放在水平地面上,在方向与水平方面成θ=37°角斜向上、大小为100N的拉力F作用下,以大小为v0=4.0m/s的速度向右做匀速直线运动,求剪断轻绳后物块A在水平地面上滑行的距离.(取当地的重力加速度(g=10m/s2,sin37°=0.6,cos37°=0.8)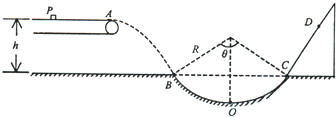 (2011?太原模拟)如图所示,传送带以一定速度沿水平匀速运动,将质量m=1.0kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧的两端点,其连线水平,轨道最低点为O,已知圆弧对应圆心角θ=106°,圆弧半径R=1.0m,A点距水平面的高度h=0.80m.小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动,0.8s时小物块第二次经过D点,已知小物块与斜面间的动摩擦因数
(2011?太原模拟)如图所示,传送带以一定速度沿水平匀速运动,将质量m=1.0kg的小物块轻轻放在传送带上的P点,物块运动到A点后被水平抛出,小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑.B、C为圆弧的两端点,其连线水平,轨道最低点为O,已知圆弧对应圆心角θ=106°,圆弧半径R=1.0m,A点距水平面的高度h=0.80m.小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动,0.8s时小物块第二次经过D点,已知小物块与斜面间的动摩擦因数