题目内容
（2011?太原模拟）为了测量运动员跃起的高度，可在弹性网上安装压力传感器，利用传感器记录运动员运动过程中对弹性网的压力，并由计算机作出压力-时间图象，如图所示．运动员在空中运动时可视为质点，则可求运动员跃起的最大高度为（g取10m/s2）（ ）分析：运动员离开弹性网后做竖直上抛运动，图中压力传感器示数为零的时间即是运动员在空中运动的时间，根据平抛运动的对称性可知，运动员竖直上抛或自由下落的时间为空中时间的一半，据此可求出运动员跃起是最大高度．
解答：解：由图可知运动员在空中的最长时间为：t=4.3s-2.3s=2s
运动员做竖直上抛运动，所以跃起最大高度为：
h=
g(
)2，将t=2s带入得：h=5m，故ACD错误，B正确．
故选B．
运动员做竖直上抛运动，所以跃起最大高度为：
h=
| 1 |
| 2 |
| t |
| 2 |
故选B．
点评：竖直上抛运动的对称性特点，是对竖直上抛运动考查的重点，要熟练掌握和应用．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
（2011?太原模拟）如图为一攀岩运动员正沿竖直岩壁缓慢攀登，由于身背较重的行囊，重心上移至肩部的0点，总质量为60kg．此时手臂与身体垂直，手臂与岩壁夹角为53°．则手受到的拉力和脚受到的作用力分别为（设手、脚受到的作用力均通过重心O，g取10m/s2，sin53°=0.8，cos53°=0.6）（ ）
（2011?太原模拟）如图所示，在离地面高为H处以水平速度v0抛出一质量为m的小球，经时间t，小球离水平地面的高度变为h，此时小球的动能为EK，重力势能为EP（选水平地面为零势能参考面）．下列图象中大致能反映小球动能Ek、势能EP变化规律的是（ ）
（2011?太原模拟）如图所示，质量为m=10kg的两个相同的物块A、B（它们之间用轻绳相连）放在水平地面上，在方向与水平方面成θ=37°角斜向上、大小为100N的拉力F作用下，以大小为v0=4.0m/s的速度向右做匀速直线运动，求剪断轻绳后物块A在水平地面上滑行的距离．（取当地的重力加速度（g=10m/s2，sin37°=0.6，cos37°=0.8）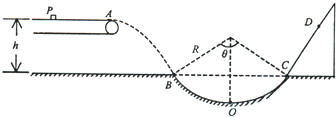
（2011?太原模拟）如图所示，传送带以一定速度沿水平匀速运动，将质量m=1.0kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、C为圆弧的两端点，其连线水平，轨道最低点为O，已知圆弧对应圆心角θ=106°，圆弧半径R=1.0m，A点距水平面的高度h=0.80m．小物块离开C点后恰好能无碰撞地沿固定斜面向上滑动，0.8s时小物块第二次经过D点，已知小物块与斜面间的动摩擦因数