题目内容
17.在正点电荷Q形成的电场中有一点P,现将电荷量q=5×10-4C的正试探电荷放到电场中的P点,q是P点受电场力的大小为F=2×10-2N,求:(1)P点电场强度E的大小;
(2)若另一试探电荷在P点受电场力的大小为F′=6×10-2N,方向沿PQ连线指向Q,那么这个电荷的电荷量q′是多少?带什么电?
分析 (1)已知试探电荷的电荷量和在电场中所受的电场力,由场强的定义式E=$\frac{F}{q}$求出E的大小.
(2)电场强度与试探电荷无关,由电场本身决定,将该试探电荷取走,同一点的场强不变.由F=qE求q′,由电场力方向与场强方向的关系判断电性.
解答 解:(1)已知 q=5×10-4C,F=2×10-2N,则P点电场强度 E=$\frac{F}{q}$=$\frac{2×1{0}^{-2}}{5×1{0}^{-4}}$=40N/C
(2)若另一试探电荷在P点受电场力的大小为F′=6×10-2N,方向沿PQ连线指向Q,说明这个电荷受到Q的引力,则这个电荷带负电.
由F′=q′E得 q′=$\frac{F′}{E}$=$\frac{6×1{0}^{-2}}{40}$=1.5×10-3C
答:
(1)P点电场强度E的大小是40N/C;
(2)这个电荷的电荷量q′是1.5×10-3C,带负电.
点评 电场强度是描述电场本身性质的物理量,是电场中最重要的概念之一,关键要掌握其定义式和方向特征.

练习册系列答案
相关题目
7.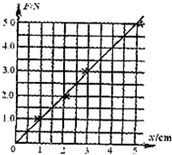 一位同学做“探究弹力大小与弹簧伸长量之间的关系”实验,测得的几组数据如表所示:
一位同学做“探究弹力大小与弹簧伸长量之间的关系”实验,测得的几组数据如表所示:
(1)计算第4组的弹簧伸长量,并将结果填在相应的位置:
②根据如表部分数据,作出弹力大小与弹簧伸长量之间的关系图线,如图所示.由图线可以判断弹力大小与弹簧伸长量成正比(选填“A.正比关系”或“B.反比关系”).
 一位同学做“探究弹力大小与弹簧伸长量之间的关系”实验,测得的几组数据如表所示:
一位同学做“探究弹力大小与弹簧伸长量之间的关系”实验,测得的几组数据如表所示:(1)计算第4组的弹簧伸长量,并将结果填在相应的位置:
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| 弹力(F/N) | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
| 弹簧原来长度(L0/cm) | 10.00 | 10.00 | 10.00 | 10.00 | 10.00 |
| 弹簧后来长度(L/cm) | 10.86 | 12.05 | 12.96 | 14.10 | 15.15 |
| 弹簧伸长量(x/cm) | 0.86 | 2.05 | 2.96 | 5.15 |
8.由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同.已知地球表面两极处的重力加速度大小为g0,在赤道处的重力加速度大小为g,地球自转的周期为T,引力常量为G.假设地球可视为质量均匀分布的球体.下列说法正确的是( )
| A. | 质量为m的物体在地球北极受到的重力大小为mg | |
| B. | 质量为m的物体在地球赤道上受到的万有引力大小为mg0 | |
| C. | 地球的半径为$\frac{({g}_{0}-g){T}^{2}}{4{π}^{2}}$ | |
| D. | 地球的密度为$\frac{3π{g}_{0}}{G{T}^{2}({g}_{0}-g)}$ |
12. 水平地面上有一辆固定着竖直绝缘管的小车,绝缘管内壁光滑,管的底部有一带正电的小球,小球的直径比管的内径略小,如图所示.小车右侧存在着垂直纸面向里的匀强磁场,现让小车始终匀速向右运动,在小球未脱离管的过程中,以下说法正确的是( )
水平地面上有一辆固定着竖直绝缘管的小车,绝缘管内壁光滑,管的底部有一带正电的小球,小球的直径比管的内径略小,如图所示.小车右侧存在着垂直纸面向里的匀强磁场,现让小车始终匀速向右运动,在小球未脱离管的过程中,以下说法正确的是( )
 水平地面上有一辆固定着竖直绝缘管的小车,绝缘管内壁光滑,管的底部有一带正电的小球,小球的直径比管的内径略小,如图所示.小车右侧存在着垂直纸面向里的匀强磁场,现让小车始终匀速向右运动,在小球未脱离管的过程中,以下说法正确的是( )
水平地面上有一辆固定着竖直绝缘管的小车,绝缘管内壁光滑,管的底部有一带正电的小球,小球的直径比管的内径略小,如图所示.小车右侧存在着垂直纸面向里的匀强磁场,现让小车始终匀速向右运动,在小球未脱离管的过程中,以下说法正确的是( )| A. | 小球对管壁一定有压力 | |
| B. | 磁场力可能对小球做正功 | |
| C. | 小球在磁场中运动的轨迹不可能是抛物线 | |
| D. | 小车进入磁场后,地面对小车的支持力一定减小 |
2.在下列运动中,加速度不变的运动有(空气阻力不计)( )
| A. | 自由落体运动 | B. | 平抛物体的运动 | ||
| C. | 竖直上抛物体运动 | D. | 匀速圆周运动 |
9. 如图为一光导纤维(可简化为一长玻璃丝)的示意图,AB表示端面,某单色平行光束照射到端面,要使光线不从玻璃丝的侧面透射出来,已知玻璃丝对该光的折射率为n,则入射角的正弦值sini应满足的条件是( )
如图为一光导纤维(可简化为一长玻璃丝)的示意图,AB表示端面,某单色平行光束照射到端面,要使光线不从玻璃丝的侧面透射出来,已知玻璃丝对该光的折射率为n,则入射角的正弦值sini应满足的条件是( )
 如图为一光导纤维(可简化为一长玻璃丝)的示意图,AB表示端面,某单色平行光束照射到端面,要使光线不从玻璃丝的侧面透射出来,已知玻璃丝对该光的折射率为n,则入射角的正弦值sini应满足的条件是( )
如图为一光导纤维(可简化为一长玻璃丝)的示意图,AB表示端面,某单色平行光束照射到端面,要使光线不从玻璃丝的侧面透射出来,已知玻璃丝对该光的折射率为n,则入射角的正弦值sini应满足的条件是( )| A. | sini>$\sqrt{{n}^{2}-1}$ | B. | sini≤$\sqrt{{n}^{2}-1}$ | C. | sini≥$\frac{\sqrt{{n}^{2}-1}}{{n}^{2}}$ | D. | sini<$\frac{\sqrt{{n}^{2}-1}}{{n}^{2}}$ |
6.当质点做匀速圆周运动时,如果外界提供的合力小于质点需要的向心力时,质点将( )
| A. | 在圆周轨道上运动 | B. | 做向心运动,离圆心越来越近 | ||
| C. | 做做匀速直线运动 | D. | 做离心运动,离圆心越来越远 |
