题目内容
8.由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同.已知地球表面两极处的重力加速度大小为g0,在赤道处的重力加速度大小为g,地球自转的周期为T,引力常量为G.假设地球可视为质量均匀分布的球体.下列说法正确的是( )| A. | 质量为m的物体在地球北极受到的重力大小为mg | |
| B. | 质量为m的物体在地球赤道上受到的万有引力大小为mg0 | |
| C. | 地球的半径为$\frac{({g}_{0}-g){T}^{2}}{4{π}^{2}}$ | |
| D. | 地球的密度为$\frac{3π{g}_{0}}{G{T}^{2}({g}_{0}-g)}$ |
分析 质量为m的物体在两极所受地球的引力等于其所受的重力.根据万有引力定律和牛顿第二定律,在赤道的物体所受地球的引力等于其在两极所受的重力联立求半径.
解答 解:A、质量为m的物体在两极所受地球的引力等于其所受的重力.F=mg0,故A错误;
B、质量为m的物体在地球赤道上受到的万有引力大小等于在地球北极受到的万有引力,即为mg0,故B正确;
C、设地球的质量为M,半径为R,在赤道处随地球做圆周运动物体的质量为m.
物体在赤道处随地球自转做圆周运动的周期等于地球自转的周期,轨道半径等于地球半径.
根据万有引力定律和牛顿第二定律有$\frac{GMm}{{R}^{2}}$-mg=m$\frac{4{π}^{2}R}{{T}^{2}}$
在赤道的物体所受地球的引力等于其在两极所受的重力即根据卫星运动的特点:越远越慢,知道在轨道Ⅱ上运动的周期小于在轨道Ⅰ上运动的周期=mg0
解得 R=$\frac{({g}_{0}-g){T}^{2}}{4{π}^{2}}$,故C正确;
D、因为$\frac{GMm}{{R}^{2}}=m{g}_{0}$,所以 M=$\frac{{g}_{0}{R}^{2}}{G}$
又因地球的体积V=$\frac{4}{3}$πR3,所以 ρ=$\frac{M}{V}=\frac{3π{g}_{0}}{G{T}^{2}({g}_{0}-g)}$,故D正确.
故选:BCD
点评 解答此题要清楚地球表面的物体受到的重力等于万有引力,根据万有引力定律和牛顿第二定律,地球近地卫星所受的万有引力提供向心力.

练习册系列答案
相关题目
18. 如图所示,我国空军在进行空中加油训练.大型加油机与接受加油的受油机在空中以同样的速度沿同一方向水平飞行.下列说法中正确的是( )
如图所示,我国空军在进行空中加油训练.大型加油机与接受加油的受油机在空中以同样的速度沿同一方向水平飞行.下列说法中正确的是( )
 如图所示,我国空军在进行空中加油训练.大型加油机与接受加油的受油机在空中以同样的速度沿同一方向水平飞行.下列说法中正确的是( )
如图所示,我国空军在进行空中加油训练.大型加油机与接受加油的受油机在空中以同样的速度沿同一方向水平飞行.下列说法中正确的是( )| A. | 选地面为参考系,受油机是静止的 | |
| B. | 选地面为参考系,加油机是静止的 | |
| C. | 选加油机为参考系,受油机是运动的 | |
| D. | 选加油机为参考系,受油机是静止的 |
19. 一根轻质弹簧未悬挂重物时,指针正对“0”刻度,在弹性限度内,当挂上40N重物时,指针指在“10”刻度,要使指针指正对“5”刻度(如图所示),应挂重物的重力( )
一根轻质弹簧未悬挂重物时,指针正对“0”刻度,在弹性限度内,当挂上40N重物时,指针指在“10”刻度,要使指针指正对“5”刻度(如图所示),应挂重物的重力( )
 一根轻质弹簧未悬挂重物时,指针正对“0”刻度,在弹性限度内,当挂上40N重物时,指针指在“10”刻度,要使指针指正对“5”刻度(如图所示),应挂重物的重力( )
一根轻质弹簧未悬挂重物时,指针正对“0”刻度,在弹性限度内,当挂上40N重物时,指针指在“10”刻度,要使指针指正对“5”刻度(如图所示),应挂重物的重力( )| A. | 10N | B. | 20N | C. | 30N | D. | 40N |
16.人走路时脚受到的摩擦力的作用,关于脚受到的摩擦力,下列说法正确的是( )
| A. | 前脚受到向前的摩擦力,后脚受到向后的摩擦力 | |
| B. | 前脚和后脚受到的摩擦力均向后 | |
| C. | 前脚受到向后的摩擦力,后脚受到向前的摩擦力 | |
| D. | 前脚和后脚受到的摩擦力都是滑动摩擦力 |
13.地球同步卫星“静止”在赤道上空的某一点,它绕地球运行的周期T1与地球自转的周期T2之间的关系是( )
| A. | T1<T2 | B. | T1>T2 | C. | T1=T2 | D. | 无法确定 |
18.关于物体所受合外力的方向与大小,下列说法正确的是( )
| A. | 物体做速率逐渐增加的直线运动时,其所受合外力的大小一定逐渐增加 | |
| B. | 物体做变速率曲线运动时,其所受合外力的方向一定改变 | |
| C. | 物体做变速率圆周运动时,其所受合外力的方向一定指向圆心 | |
| D. | 物体做匀速率曲线运动时,其所受合外力的方向总是与速度方向垂直 |
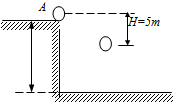 如图所示,在水平桌面上的A点有一个质量为m的物体以初速度v0=5m/s被抛出,不计空气阻力,当它到达B点时,其动能为多少?(g=10m/s2)
如图所示,在水平桌面上的A点有一个质量为m的物体以初速度v0=5m/s被抛出,不计空气阻力,当它到达B点时,其动能为多少?(g=10m/s2) 如图所示,质量为60kg的滑雪运动员,沿倾角为30°的斜坡下滑100m,若运动员运动过程中受到的阻力为80N,g取10m/s2,求这一过程中运动员所受各力做的功和总功.
如图所示,质量为60kg的滑雪运动员,沿倾角为30°的斜坡下滑100m,若运动员运动过程中受到的阻力为80N,g取10m/s2,求这一过程中运动员所受各力做的功和总功.