Question

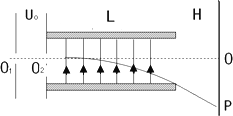
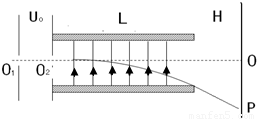
如图所示，电子质量为m，电量为e，从O₁点无初速溢出，在加速电压U₀的作用下，从O₂点水平射入平行金属板，如无其他作用，将直线打在荧光屏的O点，O₁O₂O三点沿平行金属板的中线．已知平行金属板板长为L，板间距离为d，板右边沿到荧光屏的距离为H，请计算：
①两板间加的电压U为多大时，电子恰能从板的右边沿飞出去，打在屏上的P点，并计算OP的距离．
②这种情况电子射出极板时，具有多大的速度．

Answer 1

分析：（1）对直线加速过程运用动能定理直接列式求出进如偏转电场的初速度，在偏转电场U中粒子做类似平抛运动，将运动沿着初速度方向和电场力方向正交分解，然后运用运动学公式及几何关系列式求解；
（3）对从直线加速到电偏转结束的整个运动过程运用动能定理列式求解即可．

解答：解：①电子运动轨迹如图所示

加速时由动能定理知：
eU₀=

1

2

mv₀²-0
电子在板中做类平抛L=v₀t   
 

d

2

=

1

2

at²    
 a=

Ue

md

∴

d

2

=

UL2

4U0d

 
得：U=

2U0d2

L2

电子恰从右边沿飞出，由几何关系（相似关系）知：

L 2

d 2

=

L 2 +H

OP

∴OP=（

L

2

+H）?

d

L

②对整个过程应用动能定理：e（U₀+

U

2

）=

1

2

mv²-0
得：v=

2e(U0+ U 2 ) m

=

2e(U0+ U0d2 L2 ) m

答：①两板间加的电压U为

2U0d2

L2

时，电子恰能从板的右边沿飞出去，打在屏上的P点，并计算OP的距离为（

L

2

+H）?

d

L

．
②这种情况电子射出极板时速度为

2e(U0+ U0d2 L2 ) m

．

点评：本题关键是分析清楚粒子的运动规律，对于类平抛运动，可以运用正交分解法分解为初速度方向的匀速直线运动和沿电场力方向的匀加速直线运动，同时结合动能定理列式求解．