题目内容
一只排球在A点被竖直抛出,此时动能为20J,上升到最大高度后,又回到A点,动能变为12J,假设排球在整个运动过程中受到的阻力大小恒定,A点为零势能点,则在整个运动过程中,排球的动能变为10J时,其重力势能的可能值为________、_________。
8J 8/3J
解析试题分析:由已知条件,来回过程克服阻力做功8J,即单程克服阻力做功为4J,-fh=-4J,. 对上升过程应用动能定理:-Gh-fh=0-20J,得-Gh=-16J,上升过程重力势能增加16J,即在最高点的重力势能为16J,可得:G=4f
(1)上升过程,排球动能为10J时,设上升的高度为h1,根据动能定理:-fh1-Gh1=10J-20J,由G和F关系不难算出-Gh1=-8J,即克服重力做功8J,重力势能增加8J
(2)下降过程,设下降的高度为h2, 根据动能定理:-fh2+Gh2=10J-0J,不难算出Gh2=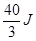 ,重力势能减少
,重力势能减少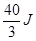 ,则该点的重力势能为
,则该点的重力势能为 。
。
考点:本题考查重力势能变化与重力做功的关系。

 发散思维新课堂系列答案
发散思维新课堂系列答案滑雪运动员沿斜坡下滑了一段距离,重力对他做功为2000J,物体克服阻力做功100J。则物体的
| A.机械能减小了100J | B.动能增加了2100J |
| C.重力势能减小了1900J | D.重力势能增加了2000J |
如图所示,桌面高为h,质量为m的小球从离桌面高H处自由落下,不计空气阻力,假设离桌面高H处重力势能为零,则小球落地前瞬间的重力势能为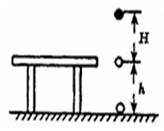
| A.mgh | B.mgH |
| C.mg(H h) | D.-mg(H+h) |
如图甲所示,abcd是位于竖直平面内的正方形闭合金属线框,金属线框的质量为m,电阻为R。在金属线框的下方有一匀强磁场区域,MN和M′N′是匀强磁场区域的水平边界,并与线框的bc边平行,磁场方向与线框平面垂直。现金属线框由距MN的某一高度从静止开始下落,图乙是金属线框由开始下落到完全穿过匀强磁场区域瞬间的速度-时间图象,图象中坐标轴上所标出的字母均为已知量。可知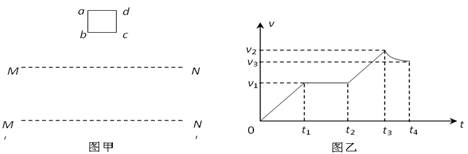
| A.金属框初始位置的bc边到边界MN的高度为v1t1 |
B.金属框的边长为 |
C.磁场的磁感应强度为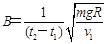 |
| D.在进入磁场过程中金属框产生的热为mgv1(t2-t1) |
下列关于功和能的说法正确的是( )
| A.功就是能,能就是功 |
| B.物体做功越多,物体的能就越大 |
| C.外力对物体不做功,这个物体就没有能量 |
| D.能量转化的多少可用功来量度 |
如图,有一宽为L足够长的光滑水平平行导轨,导轨处于竖直向上匀强磁场中,垂直导轨静止放有两根相同的金属棒,每根棒质量均为M,t =0时刻开始,给金属棒1一水平向右的外力,使金属棒1在很短时间内达到速度v0,之后保持v0不变. 此时棒1成为了一个最简单的发电机,而棒2成为了一个简单电动机,已知t = t0时刻,金属棒2也达到一个稳定的速度,且此过程中导体棒2产生焦耳热为Q,则
| A.棒2的稳定速度也为v0 |
| B.作用于棒2的安培力做正功,做的功W ="Q" |
C.外力做功为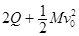 |
D.作用于棒1的安培力做负功,产生电能E=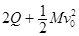 |
如图所示,回路竖直放在匀强磁场中,磁场的方向垂直于回路平面向外.导体AC可以贴着光滑竖直长导轨下滑.设回路的总电阻恒定为R,当导体AC从静止开始下落后,下面叙述中正确的说法有( )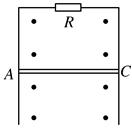
| A.导体下落过程中,机械能守恒 |
| B.导体加速下落过程中,导体减少的重力势能全部转化为在电阻上产生的热量 |
| C.导体加速下落过程中,导体减少的重力势能转化为导体增加的动能和回路中增加的内能 |
| D.导体达到稳定速度后的下落过程中,导体减少的重力势能大于回路中增加的内能 |
 。O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件
。O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件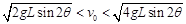 。
。