题目内容
18.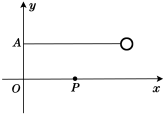 如图所示,在竖直平面内有xOy坐标系,长为l的不可伸长细绳,一端固定在A点,A点的坐标为(0、$\frac{l}{3}$),另一端系一质量为m的小球.现在x坐标轴上(x>0)固定一个小钉,拉小球使细绳绷直并呈水平位置,再让小球从静止释放,当细绳碰到钉子以后,小球可以绕钉子在竖直平面内做圆周运动.
如图所示,在竖直平面内有xOy坐标系,长为l的不可伸长细绳,一端固定在A点,A点的坐标为(0、$\frac{l}{3}$),另一端系一质量为m的小球.现在x坐标轴上(x>0)固定一个小钉,拉小球使细绳绷直并呈水平位置,再让小球从静止释放,当细绳碰到钉子以后,小球可以绕钉子在竖直平面内做圆周运动.(1)当钉子在x=-$\frac{\sqrt{3}}{3}$l的P点时,小球经过最低点时细绳承受的拉力;
(2)为使小球释放后能绕钉子在竖直平面内做圆周运动,钉子至少距O点多远.
分析 (1)由数学知识求出小球做圆周运动的轨道半径,由机械能守恒定律求出小球到达最低点时的速度,然后由牛顿第二定律求出绳子的拉力.
(2)由牛顿第二定律求出小球到达最高点的速度,由机械能守恒定律求出钉子的位置,然后确定钉子位置范围.
解答 解:(1)当钉子在x=$\frac{\sqrt{3}}{3}$l的P点时,小球绕钉子转动的半径为:
R1=l-$\sqrt{(\frac{l}{3})^{2}+{x}^{2}}$
小球由静止到最低点的过程中机械能守恒:
mg($\frac{l}{3}$+R1)=$\frac{1}{2}$mv12
在最低点细绳承受的拉力有:F-mg=m$\frac{{v}_{1}^{2}}{{R}_{1}}$
解得最大拉力为:F=5mg
(2)小球绕钉子圆周运动恰好到达最高点时,有:
mg=$\frac{{v}_{2}^{2}}{{R}_{2}}$
运动中机械能守恒:mg($\frac{l}{3}$-R2)=$\frac{1}{2}$mv22
钉子所在位置为:x'=$\sqrt{(l-{R}_{2})^{2}-(\frac{l}{3})^{2}}$
联解得:x'=$\frac{2\sqrt{10}}{9}$l
答:(1)当钉子在x=-$\frac{\sqrt{3}}{3}$l的P点时,小球经过最低点时细绳承受的拉力为5mg
(2)为使小球释放后能绕钉子在竖直平面内做圆周运动,钉子至少距O点$\frac{2\sqrt{10}}{9}$l.
点评 本题应明确小球在运动过程中只有重力做功,机械能守恒,应用机械能守恒定律与牛顿第二定律即可正确解题;解题时要注意,小球恰好到达最高点时,重力提供向心力.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
6.下列说法正确的是( )
| A. | 卢瑟福通过对α粒子散射实验现象的分析,发现了原子是可以再分的 | |
| B. | β射线与γ射线一样都是电磁波,但穿透本领远比γ射线弱 | |
| C. | 原子核的结合能等于使其完全分解成自由核子所需的最小能量 | |
| D. | 裂变时释放能量是因为发生了质量亏损 | |
| E. | 光和电子都具有波粒二象性 |
3. 如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )
如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )
 如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )
如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )| A. | (2-$\sqrt{3}$)s | B. | $\sqrt{2}$s | C. | ($\sqrt{2}$-1)s | D. | 1s |
10.在电场中某点,当放入正电荷时受到的电场力向左,以下说法中正确的是( )
| A. | 只有在该点放正电荷时,该点场强向左 | |
| B. | 只有当在该点放负电荷时,该点场强向右 | |
| C. | 该点的场强方向一定向左 | |
| D. | 该点的场强方向可能向右,也可能向左 |
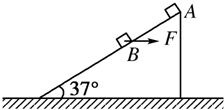 如图所示,有一足够长的斜面,倾角α=37°.一质量为m=1kg的小物块从斜面顶端A处静止下滑,到B处后,受一水平向右的恒力F作用,小物块最终停在C点(C点未画出).若AB长为2.25m,BC长为0.5m.小物块与斜面间动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2.求:
如图所示,有一足够长的斜面,倾角α=37°.一质量为m=1kg的小物块从斜面顶端A处静止下滑,到B处后,受一水平向右的恒力F作用,小物块最终停在C点(C点未画出).若AB长为2.25m,BC长为0.5m.小物块与斜面间动摩擦因数μ=0.5,sin 37°=0.6,cos 37°=0.8,g=10m/s2.求:

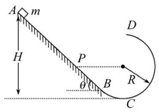 如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m的圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.g取10m/s2.求:
如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m的圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.g取10m/s2.求: